
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��0��������B��b��������������b���㣨a��2��2+|b��4|=0����ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��AB��
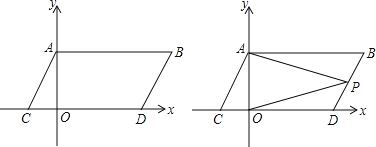
��1�����C��D�����꼰�ı���ABDC�����S�ı���ABCD
��2����y�����Ƿ����һ��M������MC��MD��ʹS��MCD=S�ı���ABDC������������һ�㣬�����M�����꣬�������ڣ���˵�����ɣ�
��3����P���߶�BD�ϵ�һ�����㣬����PA��PO������P��BD���ƶ�ʱ������B��D�غϣ�![]() ��ֵ�Ƿ����仯����˵�����ɣ�
��ֵ�Ƿ����仯����˵�����ɣ�
���𰸡���1��S�ı���ABDC=8����2�����ڣ�M��0��4����0����4������3�����䣬���ɼ�����.
��������
�����������1�����ɷǸ����������a=2��b=4���ٸ���ƽ�ƹ��ɣ��ó���C��D�����꣬Ȼ������ı���ABDC�����=AB��OA������⣻
��2�����ڣ���M����Ϊ��0��m��������S��PAB=S�ı���ABDC���г��������m��ֵ������ȷ��M�����ꣻ
��3����P����PE��AB��OC��E�㣬����ƽ���ߵ����ʵ���BAP+��DOP=��APE+��OPE=��APO���ʱ�ֵΪ1��
�⣺��1������a��2��2+|b��4|=0��
��a=2��b=4��
��A��0��2����B��4��2����
������A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D��
��C����1��0����D��3��0����
��S�ı���ABDC=AB��OA=4��2=8��
��2����y���ϴ���һ��M��ʹS��MCD=S�ı���ABCD����M����Ϊ��0��m����
��S��MCD=S�ı���ABDC��
��![]() ��4|m|=8��
��4|m|=8��
��2|m|=8��
���m=��4��
��M��0��4����0����4����
��3������P��BD���ƶ�ʱ��![]() =1���䣬�������£�
=1���䣬�������£�
����P��PE��AB��OA��E��
��CD��ABƽ�Ƶõ�����CD��AB��
��PE��CD��
���BAP=��APE����DOP=��OPE��
���BAP+��DOP=��APE+��OPE=��APO��
��![]() =1��
=1��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCֽƬ��DE�۵�������A�����ı���BCED���ⲿʱ������A����1����2֮����һ��������ϵʼ�ձ��ֲ��䣬��������һ��������ɣ��㷢�ֵĹ����ǣ� ��
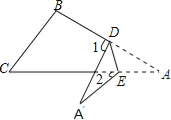
A. 2��A=��1����2 B. 3��A=2����1����2��
C. 3��A=2��1����2 D. ��A=��1����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
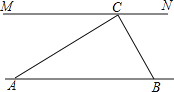
����Ŀ��Ϊ�������ѧУѧ����ѧ�����ѵ����⣬������������һ���ţ����Ź�����������ӵĿ��ȣ�����ƽ�кӰ�AB��MN֮��ľ��룩���ڲ���ʱ��ѡ���Ӷ�MN�ϵĵ�C��Ϊ�ŵ�һ�ˣ��ںӰ���A���������CAB=30�����غӰ�ABǰ��30��B������B�������CBA=60�㣬����������ϲ�����������ӵĿ��ȣ����ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73���������������
��1.73���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������⣺��һ��Ա�ƽ�У���һ��Ա���ȵ��ı�����ƽ���ı��Σ����Խ�����ƽ�ֵ��ı�����ƽ���ı��Σ������ı���ABCD�У�AB��AD��BC��DC����ô����ı���ABCD��ƽ���ı��Σ���һ��Ա���ȣ�һ��Խ���ȵ��ı�����ƽ���ı��Σ�������ȷ��������_________________���������������ϼ��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A��3x2��4x2=��1 B��3x+x=3x2
C��4xx=4x2 D����4x6��2x2=��2x3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����FPQ���ǵȱ������Σ���D��E��F�ֱ�����ABC���ߵ��е㣬��P��AB���ϣ�����EF��QE����AB=6��PB=1����QE= ��
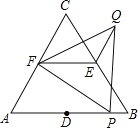
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ�У���֪A��3��4����B��3����1����C����3����2����D����2��3��
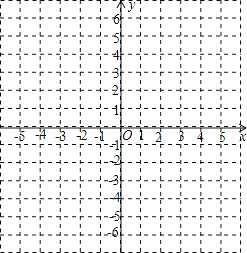
��1����ͼ�ϻ����ı���ABCD�������ı���ABCD�������
��2����PΪ�ı���ABCD����һ�㣬��֪P����Ϊ����1��1�������ı���ABCDͨ��ƽ�ƺ�P�������Ϊ��2����2��������ƽ�ƵĹ�����ֱ��д���ı���ABCDƽ�ƺ���ĸ���������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ɽֲ��������A��B����������֪A��Ϊ�����Σ���Ϊ��x+y���ף���Ϊ��x��y���ף�B��Ϊ�����Σ��߳�Ϊ��x+3y���ף�
��1�����ô���ʽ��ʾA��B���������֮�Ͳ�����
��2���ָ���ʵ����Ҫ��A���������ģ������ӣ�11x��y���ף������٣�x��2y���ף����ĺ�A���ij��ȿ���350�ף������ĺ��������ܳ�֮��Ϊ980�ף�
����x��y��ֵ��
����A��ȫ����ֲC�ֻ���B��ȫ����ֲD�ֻ�����C��D���ֻ�Ͷ��ķ����������ο͵����������

�����ĺ�A��B�������εľ�����֮�ͣ���������=���橁Ͷ�룩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽�������ã�
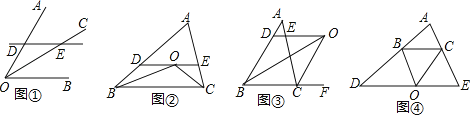
��1������ͼ�Σ���ͼ������֪OC����AOB�Ľ�ƽ���ߣ�DE��OB���ֱ�OA��OC�ڵ�D��E����֤��DE=OD��
��2����ͼ�����ҳ������Ļ���ͼ�Σ������ã�1���еĹ��ɽ��������⣺��֪��ABC�У������ڽ���ABC����ACB��ƽ���߽��ڵ�O������O��DE��BC����AB��AC�ڵ�D��E����֤��DE=BD+CE��
��3������ͼ���������ڽǵĽ�ƽ���߸�Ϊһ���ڽǣ���ͼ������ABC����һ����ǣ���ACF��������������ǣ���ͼ����DBC����BCE���Ľ�ƽ���ߣ������������䣬���߶�DE��BD��CE��������ϵ�ֱ��ǣ�ͼ��Ϊ ��ͼ��Ϊ ����������ѡһ������֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com