
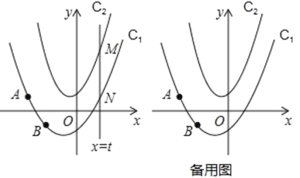
【题目】如图,在平面直角坐标系中,抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.
(1)求抛物线C1的表达式;
(2)直接用含t的代数式表达线段MN的长;
(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值.
【答案】(1)y=x2+x﹣1;(2)MN=t2+2;(3)t=0或1
【解析】
(1)将点A、B的坐标代入抛物线表达式,即可求解;
(2)点M、N的坐标分别为:(t,2t2+t+1)、(t,t2+t-1),即可求解;
(3)分∠ANM=90°、∠AMN=90°两种情况,分别求解即可.
解:(1)将点A、B的坐标代入抛物线表达式得:![]() ,解得:
,解得:![]() ,
,
故抛物线C1的表达式为:y=x2+x﹣1;
(2)点M、N的坐标分别为:(t,2t2+t+1)、(t,t2+t﹣1),
则MN=(2t2+t+1)﹣(t2+t﹣1)=t2+2;
(3)①当∠ANM=90°时,AN=MN,
AN=t﹣(﹣2)=t+2,MN=t2+2,
t=t2+2,解得:t=0或1(舍去0),故t=1;
②当∠AMN=90°时,AM=MN,
AM=t+2=MN=t2+2,
解得:t=0或1(舍去1),故t=1;
综上,t=0或1.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】种植草莓大户张华现有22吨草莓等待出售,有两种销售渠道,一是运往省城直接批发给零售商,二是在本地市场零售,受客观因素影响,张华每天只能采用一种销售渠道,而且草莓必须在10天内售出(含10天)经过调查分析,这两种销售渠道每天销量及每吨所获纯利润见右表:
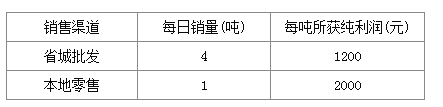
(1)若一部分草莓运往省城批发给零售商,其余在本地市场零售,请写出销售22吨草莓所获纯利润y(元)与运往省城直接批发零售商的草莓量x(吨)之间的函数关系式;
(2)怎样安排这22吨草莓的销售渠道,才使张华所获纯利润最大?并求出最大纯利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,BC=16,点D为BC边上的一个动点(点D不与点B、点C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F.
(1)求证:ABCE=BDCD;
(2)当DF平分∠ADC时,求AE的长;
(3)当△AEF是等腰三角形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
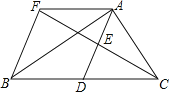
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若BA⊥AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.
(1)求抛物线的表达式;
(2)设抛物线的对称轴为l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
(3)如图2,连接BC,PB,PC,设△PBC的面积为S.
①求S关于t的函数表达式;
②求P点到直线BC的距离的最大值,并求出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
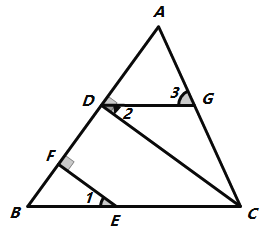
【题目】如图,在△ABC中,CD⊥AB,垂足为D. 点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求的∠3度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图: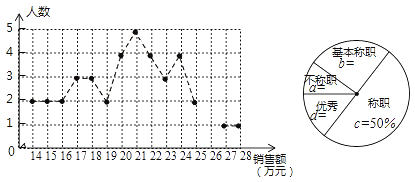
设销售员的月销售额为x(单位:万元)。销售部规定:当x<16时,为“不称职”,当 ![]() 时为“基本称职”,当
时为“基本称职”,当![]() 时为“称职”,当
时为“称职”,当![]() 时为“优秀”.根据以上信息,解答下列问题:
时为“优秀”.根据以上信息,解答下列问题:
(1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个转盘被分成![]() 等分,每一份上各写有一个数字,随机转动转盘
等分,每一份上各写有一个数字,随机转动转盘![]() 次,第一次转到的数字数字为十位数字,第二次转到的数字为个位数字,
次,第一次转到的数字数字为十位数字,第二次转到的数字为个位数字,![]() 次转动后组成一个两位数(若指针停在等分线上则重新转一次)
次转动后组成一个两位数(若指针停在等分线上则重新转一次)
![]() 用画树状图的方法求出转动后所有可能出现的两位数的个数.
用画树状图的方法求出转动后所有可能出现的两位数的个数.
![]() 甲、乙两人做游戏,约定得到的两位数是偶数时甲胜,否则乙胜,这个游戏公平吗?请说明理由.
甲、乙两人做游戏,约定得到的两位数是偶数时甲胜,否则乙胜,这个游戏公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
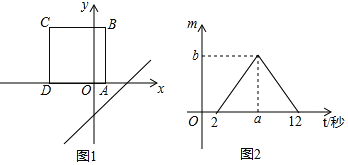
【题目】如图1,将正方形ABCD按图1所示置于平面直角坐标系中,AD边与x轴重合,顶点B,C位于x轴上方,将直线l:y=x﹣3沿x轴向左以每秒1个单位长度的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t秒,m与t的函数图象如图2所示,则a,b的值分别是( )
A.6,![]() B.6,
B.6,![]() C.7,7
C.7,7![]() D.7,5
D.7,5![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com