
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若BA⊥AC,试判断四边形AFBD的形状,并证明你的结论.
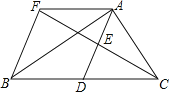
【答案】(1)详见解析;(2)四边形AFBD是菱形,理由详见解析.
【解析】
(1)首先推知△AFE≌△DCE(AAS),则其对应边相等AF=CD,结合已知条件AF=BD得到:BD=CD,即D是BC的中点;
(2)四边形AFBD是菱形.连接FD.构造平行四边形AFDC.根据对角线相互垂直的平行四边形是菱形证得结论:四边形AFBD是菱形.
(1)证明:∵AF∥BC,
∴∠AFE=∠DCE,∠FAE=∠CDE.
∵E为AD的中点,
∴AE=DE.
∴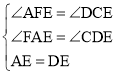 ,
,
∴△AFE≌△DCE(AAS).
∴AF=CD.
∵AF=BD,
∴BD=CD,即D是BC的中点;
(2)四边形AFBD是菱形.理由如下:
连接FD.∵AF∥BD且AF=BD,
∴四边形AFBD是平行四边形.
同理可证四边形AFDC是平行四边形.
∴FD∥AC.
∵BA⊥AC,
∴BA⊥FD.
∴四边形AFBD是菱形.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
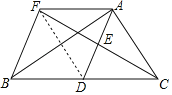
【题目】如图,已知AB是⊙O的直径,BE是⊙O的弦,BC是∠ABE的平分线且交⊙O于点C,连接AC,CE,过点C作CD⊥BE,交BE的延长线于点D.
(1)∠DCE ∠CBE;(填“>”“<”或“=”)
(2)求证:DC是⊙O的切线;
(3)若⊙O的直径为10,sin∠BAC=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一项工程,由甲、乙两个工程队共同完成,若乙工程队单独完成需要60天;若两个工程队合作18天后,甲工程队再单独做10天也恰好完成.
(1)甲工程队单独完成此项工程需要几天?
(2)若甲工程队每天施工费用为0.6万元,乙工程队每天施工费用为0.35万元,要使该项目总施工费用不超过22万元,则乙工程队至少施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
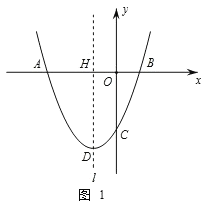
【题目】如图1,已知抛物线![]() 经过A(-3,0),B(1,0),C(0,-3)三点,其顶点为D,对称轴是直线
经过A(-3,0),B(1,0),C(0,-3)三点,其顶点为D,对称轴是直线![]() ,
,![]() 与x轴交于点H.
与x轴交于点H.
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴![]() 上的一个动点,求△PBC周长的最小值;
上的一个动点,求△PBC周长的最小值;
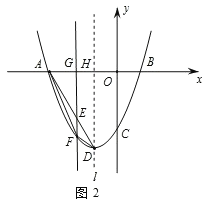
(3)如图2,若E是线段AD上的一个动点(E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①试求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
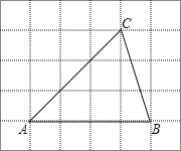
【题目】如图,将![]() 放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
![]() Ⅰ
Ⅰ![]() 的面积等于______;
的面积等于______;
![]() Ⅱ
Ⅱ![]() 若四边形DEFG是
若四边形DEFG是![]() 中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法
中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法![]() 不要求证明
不要求证明![]() ________________.
________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个运输小队分别从两个仓库以相同的工作效率调运一批物资,两队同时开始工作.第二小队工作5天后,由于技术问题检修设备5天,为赶上进度,再次开工后他们将工作效率提高到原先的2倍,结果和第一小队同时完成任务.在两队调运物资的过程中,两个仓库物资的剩余量y t与第一小队工作时间x天的函数图像如图所示.

(1)①求线段AC所表示的y与x之间的函数表达式;
②求点F的坐标,并解释点F的实际意义.
(2)如果第二小队没有检修设备,按原来的工作效率正常工作,那么他们完成任务的天数是 天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解某学校大班额现状,某市决定通过新建学校来解决该问题.经测算,建设6个小学,5个中学,需费用13800万元,建设10个小学,7个中学,需花费20600万元.
(1)求建设一个小学,一个中学各需多少费用.
(2)该市共计划建设中小学80所,其中小学的建设数量不超过中学建设数量的1.5倍.设建设小学的数量为x个,建设中小学校的总费用为y万元.
①求y关于x的函数关系式;
②如何安排中小学的建设数量,才能使建设总费用最低?
(3)受国家开放二胎政策及外来务工子女就读的影响,预计在小学就读人数会有明显增加,现决定在(2)中所定的方案上增加投资以扩大小学的就读规模,若建设小学总费用不超过建设中学的总费用,则每所小学最多可增加多少费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点P和图形M,给出如下定义:Q为图形M上任意一点,如果
中的点P和图形M,给出如下定义:Q为图形M上任意一点,如果![]() 两点间的距离有最大值,那么称这个最大值为点P与图形M间的开距离,记作
两点间的距离有最大值,那么称这个最大值为点P与图形M间的开距离,记作![]() .已知直线
.已知直线![]() 与x轴交于点A,与y轴交于点B,
与x轴交于点A,与y轴交于点B,![]() 的半径为1.
的半径为1.
(1)若![]() ,
,
①求![]() 的值;
的值;
②若点C在直线![]() 上,求
上,求![]() 的最小值;
的最小值;
(2)以点A为中心,将线段![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,点E在线段
,点E在线段![]() 组成的图形上,若对于任意点E,总有
组成的图形上,若对于任意点E,总有![]() ,直接写出b的取值范围.
,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点.
是抛物线的顶点.
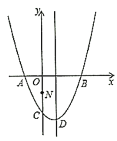
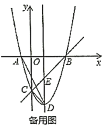
(1)求抛物线的解析式.
(2)点![]() 是
是![]() 轴负半轴上的一点,且
轴负半轴上的一点,且![]() ,点
,点![]() 在对称轴右侧的抛物线上运动,连接
在对称轴右侧的抛物线上运动,连接![]() ,
,![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() ,连接
,连接![]() ,当
,当![]() 平分
平分![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(3)直线![]() 交对称轴于点
交对称轴于点![]() ,
,![]() 是坐标平面内一点,请直接写出
是坐标平面内一点,请直接写出![]() 与
与![]() 全等时点
全等时点![]() 的坐标__________.
的坐标__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com