
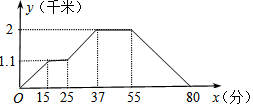
 如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )
如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )| A. | 1.1,0.08 | B. | 1.1,0.025 | C. | 0.9,0.08 | D. | 0.9,0.025 |
科目:初中数学 来源: 题型:解答题
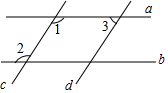 请将下列解答过程补充完整.
请将下列解答过程补充完整.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
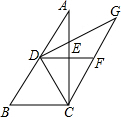 如图,在△ABC中,∠ACB=90°,∠B>∠A,AE=EC,∠A=∠DCA,CF∥AB交DE的延长线于点F.
如图,在△ABC中,∠ACB=90°,∠B>∠A,AE=EC,∠A=∠DCA,CF∥AB交DE的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(亩) | 20 | 25 | 30 | 35 |
| y(元) | 1800 | 1700 | 1600 | 1500 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$是有理数 | B. | 面积为5的正方形边长是$\sqrt{5}$ | ||
| C. | $\sqrt{5}$介于2和3之间 | D. | 在数轴上可以找到表示$\sqrt{5}$的点 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
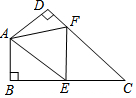 在四边形ABCD中∠C=55°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△EAF周长最小时,∠EAF的度数为( )
在四边形ABCD中∠C=55°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△EAF周长最小时,∠EAF的度数为( )| A. | 55° | B. | 70° | C. | 125° | D. | 110° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC,∠BAC=90°,D,E分别为AB,BC的中点,点F在CA的延长线上,∠FDA=∠B.
如图,Rt△ABC,∠BAC=90°,D,E分别为AB,BC的中点,点F在CA的延长线上,∠FDA=∠B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com