
| x(亩) | 20 | 25 | 30 | 35 |
| y(元) | 1800 | 1700 | 1600 | 1500 |
分析 (1)待定系数法求解可得;
(2)根据总利润=每亩利润×亩数,分0<x≤15和15<x≤110两种情况分别求解可得.
解答 解:(1)设y=kx+b,
将x=20、y=1800和x=30、y=1600代入得:$\left\{\begin{array}{l}{20k+b=1800}\\{30k+b=1600}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-20}\\{b=2200}\end{array}\right.$,
∴y=-20x+2200,
∵-20x+2200≥0,
解得:x≤110,
∴15<x≤110;
(2)当0<x≤15时,W=1900x,
∴当x=15时,W最大=28500元;
当15<x≤110时,W=(-20x+2200)x=-20x2+2200x=-20(x-55)2+60500,
∵x≤60,
∴当x=55时,W最大=60500元,
综上,小王家承包55亩荒山获得的总利润最大,并求总利润W的最大值为60500元.
点评 本题主要考查二次函数的应用,熟练掌握待定系数法和由题意依据相等关系列出函数解析式是解题的关键.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:填空题
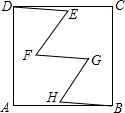 如图,在正方形ABCD中,点E,F,G,H均在其内部,且DE=EF=FG=GH=HB=1,∠E=∠F=∠G=∠H=60°,则AB=$\sqrt{7}$.
如图,在正方形ABCD中,点E,F,G,H均在其内部,且DE=EF=FG=GH=HB=1,∠E=∠F=∠G=∠H=60°,则AB=$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
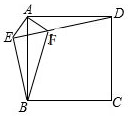 如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AF⊥AE交DE于点F,已知AE=AF=1,BF=$\sqrt{5}$
如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AF⊥AE交DE于点F,已知AE=AF=1,BF=$\sqrt{5}$查看答案和解析>>
科目:初中数学 来源: 题型:选择题
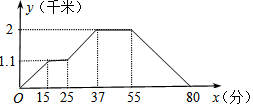 如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )
如图,小强从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小强离他家的距离,小强家、菜地、玉米地在同一直线上.如果菜地和玉米地的距离为a千米,小强从玉米地回家的平均速度为b千米/分,则a、b的值分别为( )| A. | 1.1,0.08 | B. | 1.1,0.025 | C. | 0.9,0.08 | D. | 0.9,0.025 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com