
(本小题满分12分) 如图① 已知抛物线 (
( ≠0)与x轴交于点A(1,0)和点B (-3,0),与y轴交于点C.
≠0)与x轴交于点A(1,0)和点B (-3,0),与y轴交于点C.

(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点N ,问在对称轴上是否存在点P,使△CNP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
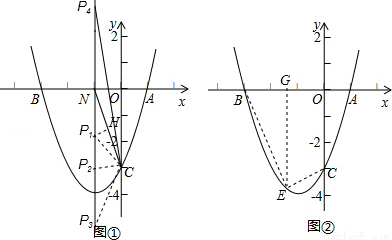
(3)如图②,若点E为第三象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
(1) 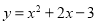 ; (2)存在, P(-1,
; (2)存在, P(-1, ),P(-1,-
),P(-1,-  ),P(-1,-6),P(-1,-
),P(-1,-6),P(-1,- );(3)
);(3)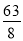 ,E(
,E(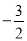 ,
,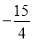 ).
).
【解析】
试题分析:(1)由抛物线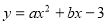 (a≠0)点A(1,0)和点B (﹣3,0),由待定系数法就可以直接求出a、b的值而求出抛物线的解析式;
(a≠0)点A(1,0)和点B (﹣3,0),由待定系数法就可以直接求出a、b的值而求出抛物线的解析式;
(2)由(1)的解析式就可以求出C点的坐标,求出OC的值,在Rt△CON中由勾股定理就可以求出CN的值,CP1=NP1时,作P1H⊥CN于H,由三角形相似就可以求出P1N的值,从而求出P1的坐标;
(3)设出点E的坐标,连接BE、CE,作EG⊥OB于点G,就可以表示EG、BG、OG的值就可以表示出四边形BOCE的面积,然后化为顶点式就可以求出其面积的最大值.
试题解析:(1)如图①,
∵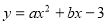 (a≠0)与x轴交于点A(1,0)和点B (﹣3,0),
(a≠0)与x轴交于点A(1,0)和点B (﹣3,0),
∴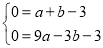 ,解得:
,解得: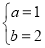 ,∴
,∴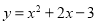 ;
;
(2)∵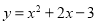 ,∴
,∴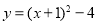 ,∴N(﹣1,0),∴ON=1.
,∴N(﹣1,0),∴ON=1.
∴当x=0时,y=﹣3,∴C(0,﹣3),∴OC=3.
在Rt△CON中,由勾股定理,得:CN=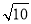 ,
,
当P1N=P1C时,△P1NC是等腰三角形,作P1H⊥CN,
∴NH=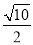 ,△P1HN∽△NOC,∴
,△P1HN∽△NOC,∴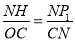 ,∴
,∴ ,∴NP1=
,∴NP1=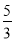 ,∴P1(﹣1,
,∴P1(﹣1,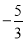 ),
),
当P4N=CN时,P4N=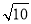 ,∴P4(﹣1,
,∴P4(﹣1,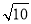 ),
),
当P2N=CN时,P2N=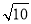 ,∴P2(﹣1,﹣
,∴P2(﹣1,﹣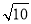 ),
),
当P3C=CN时,P3N=6,∴P3(﹣1,﹣6)
∴P点的坐标为:(﹣1,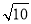 )、(﹣1,﹣
)、(﹣1,﹣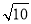 )、(﹣1,﹣6)和(﹣1,
)、(﹣1,﹣6)和(﹣1,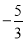 );
);
(3)设E(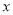 ,
,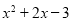 ),连接BE、CE,作EG⊥OB于点G,
),连接BE、CE,作EG⊥OB于点G,
∴GO=﹣x,BG=x+3,GE=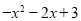 ,
,
∴S=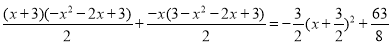 ,
,
∴x=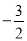 ,S最大值=
,S最大值=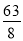 ,
,
当x=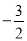 时,
时,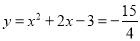 ,
,
∴E(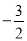 ,
,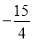 ).
).
考点:1.二次函数综合题;2.等腰三角形的性质.


科目:初中数学 来源:2014-2015学年云南省九年级上学期期中考试数学试卷(解析版) 题型:选择题
已知二次函数 的图象与x轴的一个交点为(1,0)则关于x的一元二次方程
的图象与x轴的一个交点为(1,0)则关于x的一元二次方程 的两实数根是( )
的两实数根是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省八年级上学期期中数学试卷(解析版) 题型:解答题
如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF,求证:∠A=∠D

查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省腾冲县九年级上学期五校联考摸底考试数学试卷(解析版) 题型:填空题
在Rt△ABC中,∠C=90°,sinB= ,则
,则 =________________;
=________________;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省腾冲县九年级上学期五校联考摸底考试数学试卷(解析版) 题型:计算题
(本题共4道小题,每小题5分,满分20分)
(1)解方程:
(2)分解因式:
(3)计算:
(4)先化简,再求值: ,其中
,其中 .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市七年级上学期第一次质量检测数学试卷(解析版) 题型:选择题
下列各组运算中,运算后结果相等的是( )
A. 与
与 B.
B. 与
与 C.
C. 与
与 D.
D. 与
与
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市七年级上学期第一次质量检测数学试卷(解析版) 题型:填空题
我国的国土面积约为9600000 ,用科学记数法写成约为_________
,用科学记数法写成约为_________  .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com