
分析 先根据不等式的基本性质把不等式去分母、去括号、再移项、合并同类项求出x的取值范围,再与已知解集相比较即可求出m的取值范围.
解答 解:去括号得:$\frac{1}{2}x-\frac{1}{2}m>3-\frac{3}{2}m$
移项得:$\frac{1}{2}x>3-\frac{3}{2}m+\frac{1}{2}m$
合并同类项得;$\frac{1}{2}x>3-m$
系数化为1得;x>6-2m,
∵不等式的解集为x>3.
∴6-2m=3.
解得:m=$\frac{3}{2}$
故答案为:$\frac{3}{2}$.
点评 考查了解一元一次不等式,和解一元一次方程组,根据不等式的解集为x>3列出关于m的方程是解题的关键.


科目:初中数学 来源: 题型:解答题
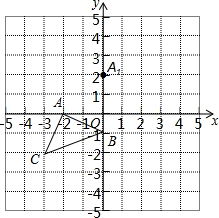 将6×6的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,三角形ABC的顶点和点A,都在格点上.
将6×6的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,三角形ABC的顶点和点A,都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
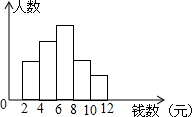 某校七(1)班有48人,对本班学生展开零花钱的消费调查,绘制了如图的频数分布直方图,已知从左到右小长方形高之比为2:3:4:2:1,则零花钱在8元以上的共有12人.
某校七(1)班有48人,对本班学生展开零花钱的消费调查,绘制了如图的频数分布直方图,已知从左到右小长方形高之比为2:3:4:2:1,则零花钱在8元以上的共有12人.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
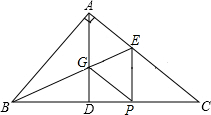 如图,在Rt△ABC中,AD是高线,BE平分∠ABC交AC于E,交AD于G,过E作EP⊥BC于P,连接GP,请问四边形AGPE是什么四边形?为什么?
如图,在Rt△ABC中,AD是高线,BE平分∠ABC交AC于E,交AD于G,过E作EP⊥BC于P,连接GP,请问四边形AGPE是什么四边形?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com