
| 次数 m | 余额 n(元) |
| 1 | 50-0.9 |
| 2 | 50-1.8 |
| 3 | 50-2.7 |
| 4 | 50-3.6 |
| … | … |
分析 (1)根据记录的余额,可判断每次乘车的费用为0.9元,若乘车的次数m,则余额n为50减去0.9m;
(2)把m=10代入(1)中的关系式中计算出对应的代数式的值即可;
(3)先用50除以0.9约为55次,再计算出55次的余额,由于余额小于0.9,则可判断小强最多能乘55次车.
解答 解:(1)n=50-0.9m;
(2)当m=10时,n=50-0.9×10=41(元);
(3)50÷0.9≈55(次),
当m=55时,n=50-0.9×55=0.5(元)
而0.5<0.9,
所以小强最多能乘55次车.
点评 本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.本题的关键是通过表格中的数据得到每次乘车的费用为0.9元.


科目:初中数学 来源: 题型:解答题
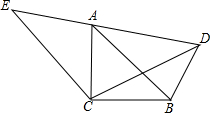 已知:如图△ACB与△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上.请证明:
已知:如图△ACB与△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上.请证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
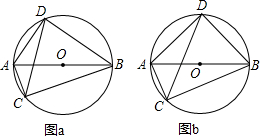
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a的倒数是$\frac{1}{a}$ | B. | 任何有理数都有倒数 | ||
| C. | -$\frac{1}{4}$的倒数是-4 | D. | $\frac{1}{2}$的倒数是-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
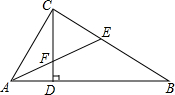 如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm,求:
如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm,求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com