
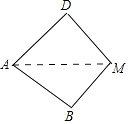
【题目】已知:如图1,图形①满足AD=AB,MD=MB,∠A=72°,∠M=144°.图形②与图形①恰好拼成一个菱形(如图2).记AB的长度为a,BM的长度为b. 

(1)图形①中∠B=°,图形②中∠E=°;
(2)小明有两种纸片各若干张,其中一种纸片的形状及大小与图形①相同,这种纸片称为“风筝一号”;另一种纸片的形状及大小与图形②相同,这种纸片称为“飞镖一号”. ①小明仅用“风筝一号”纸片拼成一个边长为b的正十边形,需要这种纸片张;
【答案】
(1)72;36
(2)5 ②小明若用若干张“风筝一号”纸片和“飞镖一号”纸片拼成一个“大风筝”(如图3),其中∠P=72°,∠Q=144°,且PI=PJ=a+b,IQ=JQ.请你在图3中画出拼接线并保留画图痕迹.(本题中均为无重叠、无缝隙拼接)
根据题意可知:“风筝一号”纸片用两张和“飞镖一号”纸片用一张,
画出拼接线如图所示: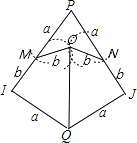
【解析】解:(1)连接AM,如图所示: ∵AD=AB,DM=BM,AM为公共边,
∴△ADM≌△ABM,
∴∠D=∠B,
又因为四边形ABMD的内角和等于360°,∠DAB=72°,∠DMB=144°,
∴∠B= ![]() =72°;
=72°;
在图2中,因为四边形ABCD为菱形,所以AB∥CD,
∴∠A+∠ADC=∠A+∠ADM+∠CEF=180°,∠A=72°,∠ADM=72°,
∴∠CEF=180°﹣72°﹣72°=36°;
2)①用“风筝一号”纸片拼成一个边长为b的正十边形,
得到“风筝一号”纸片的点A与正十边形的中心重合,又∠A=72°,
则需要这种纸片的数量= ![]() =5;
=5;
②根据题意可知:“风筝一号”纸片用两张和“飞镖一号”纸片用一张,
画出拼接线如图所示:
所以答案是:(1)72°;36°;(2)①、5.
【考点精析】本题主要考查了菱形的性质和正多边形和圆的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.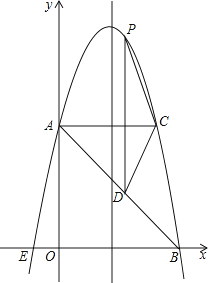
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行与y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120m,则这栋楼的高度为( )
A.160 ![]() m
m
B.120 ![]() m
m
C.300m
D.160 ![]() m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB. 
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古运河是扬州的母亲河.为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两工程队先后接力完成.A工程队每天整治12米,B工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下: 甲: ![]() ;乙:
;乙: 
根据甲、乙两名问学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示 , y表示;
乙:x表示 , y表示 .
(2)求A、B两工程队分别整治河道多少米.(写出完整的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=﹣x+7与正比例函数y= ![]() x的图象交于点A,且与x轴交于点B.
x的图象交于点A,且与x轴交于点B.
(1)求点A和点B的坐标;
(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O﹣C﹣A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象. 
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com