
����Ŀ����ͼ����֪һ�κ���y=��x+7������������y= ![]() x��ͼ���ڵ�A������x�ύ�ڵ�B��
x��ͼ���ڵ�A������x�ύ�ڵ�B��
��1�����A�͵�B�����ꣻ
��2������A��AC��y���ڵ�C������B��ֱ��l��y�ᣮ����P�ӵ�O��������ÿ��1����λ�����ٶȣ���O��C��A��·�����A�˶���ͬʱֱ��l�ӵ�B����������ͬ�ٶ�����ƽ�ƣ���ƽ�ƹ����У�ֱ��l��x���ڵ�R�����߶�BA���߶�AO�ڵ�Q������P�����Aʱ����P��ֱ��l��ֹͣ�˶������˶������У��趯��P�˶���ʱ��Ϊt�룮
�ٵ�tΪ��ֵʱ����A��P��RΪ����������ε����Ϊ8��
���Ƿ������A��P��QΪ������������ǵ��������Σ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��һ�κ���y=��x+7������������y= ![]() x��ͼ���ڵ�A������x�ύ�ڵ�B��
x��ͼ���ڵ�A������x�ύ�ڵ�B��
�� 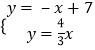 ��
��
��ã� ![]() ��
��
��A����������3��4����
��y=��x+7=0��
��ã�x=7��
��B����������7��0��
��2��
�⣺�ٵ�P��OC���˶�ʱ��0��t��4ʱ��PO=t��PC=4��t��BR=t��OR=7��t��
�ߵ���A��P��RΪ����������ε����Ϊ8��
��S����ACOB��S��ACP��S��POR��S��ARB=8��
�� ![]() ��AC+BO����CO��
��AC+BO����CO�� ![]() AC��CP��
AC��CP�� ![]() PO��RO��
PO��RO�� ![]() AM��BR=8��
AM��BR=8��
�ࣨAC+BO����CO��AC��CP��PO��RO��AM��BR=16��
�ࣨ3+7����4��3����4��t����t����7��t����4t=16��
��t2��8t+12=0��
��ã�t1=2��t2=6����ȥ����
��t=4ʱ�������������Σ�
��4��t��7ʱ��S��APR= ![]() AP��OC=2��7��t��=8�����t=3��������4��t��7��
AP��OC=2��7��t��=8�����t=3��������4��t��7��
������������t=2ʱ����A��P��RΪ����������ε����Ϊ8��
�ڴ��ڣ��ӳ�CA��ֱ��l����һ��D����l��AB�ཻ��Q��
��һ�κ���y=��x+7��x�ύ�ڣ�7��0���㣬��y�ύ�ڣ�0��7���㣬
��NO=OB��
���OBN=��ONB=45�㣬
��ֱ��l��y�ᣬ
��RQ=RB��CD��L��
��0��t��4ʱ����ͼ1��
RB=OP=QR=t��DQ=AD=��4��t����AC=3��PC=4��t��
����A��P��QΪ������������ǵ��������Σ���AP=AQ��
��AC2+PC2=AP2=AQ2=2AD2��
��9+��4��t��2=2��4��t��2����ã�t1=1��t2=7����ȥ����
��AP=PQʱ 32+��4��t��2=��7��t��2��
���t=4 ����ȥ��
��PQ=AQʱ��2��4��t��2=��7��t��2��
���t1=1+3 ![]() ����ȥ����t2=1��3
����ȥ����t2=1��3 ![]() ����ȥ����
����ȥ����
��t=4ʱ�������������Σ�
��4��t��7ʱ����ͼ������ͼ������A��AD��OB��D����AD=BD=4��
��ֱ��l��AC��E����QE��AC��AE=RD=t��4��AP=7��t��
��cos��OAC= ![]() =
= ![]() ��
��
��AQ= ![]() ��t��4����
��t��4����
��AQ=AP���� ![]() ��t��4��=7��t�����t=
��t��4��=7��t�����t= ![]() ��
��
��AQ=PQʱ��AE=PE����AE= ![]() AP��
AP��
��t��4= ![]() ��7��t����
��7��t����
��ã�t=5��
��AP=PQʱ����P��PF��AQ��F��
AF= ![]() AQ=
AQ= ![]() ��
�� ![]() ��t��4����
��t��4����
��Rt��APF����cos��PAF= ![]() =
= ![]() ��
��
��AF= ![]() AP��
AP��
�� ![]() ��
�� ![]() ��t��4��=
��t��4��= ![]() ��7��t����
��7��t����
��ã�t= ![]() ��
��
������������t=1��5�� ![]() ��
�� ![]() ʱ��������A��P��QΪ������������ǵ��������Σ�
ʱ��������A��P��QΪ������������ǵ��������Σ�

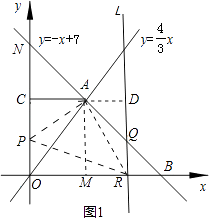
����������1������ͼ���������ύ����ֱ�ӵó����ɣ�������ֱ�߽�����������ֱ�߽���ʽ�������ɵó��������ꣻ��2��������S����ACOB��S��ACP��S��POR��S��ARB=8����ʾ�������ֵı߳���������һԪ���η��̣�������ɣ��ڸ���һ�κ�����������Ľ���ó�����OBN=��ONB=45�㣬�������ù��ɶ����Լ����������ε����ʺ�ֱ�������ε��ж�������ɣ�
�����㾫��������һ�κ�����ͼ������ʺ͵��������ε������ǽ����ĸ�������Ҫ֪��һ�κ�����ֱ�ߣ�ͼ�������ޣ���������������,����ԭ��һֱ�ߣ�����ϵ��k��b,����֮��ĪС����k��б�ʶ��н�,b��Y�������,kΪ��������б,x����y������kΪ��������չ,�仯�������෴��k�ľ���ֵԽ��,��������ԽԶ�����������ε���������ȣ���ƣ��ȱ߶ԵȽǣ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ1��ͼ������AD=AB��MD=MB����A=72�㣬��M=144�㣮ͼ����ͼ��ǡ��ƴ��һ�����Σ���ͼ2������AB�ij���Ϊa��BM�ij���Ϊb�� 

��1��ͼ���С�B=�㣬ͼ���С�E=�㣻
��2��С��������ֽƬ�������ţ�����һ��ֽƬ����״����С��ͼ����ͬ������ֽƬ��Ϊ������һ�š�����һ��ֽƬ����״����С��ͼ����ͬ������ֽƬ��Ϊ������һ�š��� ��С�����á�����һ�š�ֽƬƴ��һ���߳�Ϊb����ʮ���Σ���Ҫ����ֽƬ�ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���BAC=90�㣬AB��AC��M��BC�ߵ��е㣬MN��BC��AC�ڵ�N������P�ӵ�B����������BA��ÿ�� ![]() �����ٶ��˶���ͬʱ������Q�ӵ�N����������NC�˶�����ʼ�ձ���MQ�AMP�����˶�ʱ��Ϊt�루t��0����
�����ٶ��˶���ͬʱ������Q�ӵ�N����������NC�˶�����ʼ�ձ���MQ�AMP�����˶�ʱ��Ϊt�루t��0����
��1����PBM���QNM��������ͼ1Ϊ��˵�����ɣ�
��2������ABC=60�㣬AB=4 ![]() ���ף� ����Q���˶��ٶȣ�
���ף� ����Q���˶��ٶȣ�
�����APQ�����ΪS��ƽ�����ף�����S��t�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������֮�俪ͨ�˶���������г�����֪ÿ��2h��һ���ٶ���ͬ�Ķ������г��Ӽ׳ǿ����ҳǣ���ͼ��OA�ǵ�һ�ж������г��뿪�׳ǵ�·��s��km��������ʱ��t��h���ĺ���ͼ��BC��һ�д��ҳǿ����׳ǵ���ͨ�쳵��׳ǵ�·��s��km��������ʱ��t��h���ĺ���ͼ�������ͼ�е���Ϣ������������⣺
��1����ͼ����ͨ�쳵����ʱ��ȵ�һ�ж������г�����ʱ���� �� 1h������������������������B��������600��ʵ���������� ����
��2����ֱ����ͼ�л����ڶ��ж������г��뿪�׳ǵ�·��s��km����ʱ��t��h���ĺ���ͼ����
��3������ͨ�쳵���ٶ�Ϊ100km/h��
����ڶ��ж������г������ʱ�������ͨ�쳵������
����ֱ��д��������ͨ�쳵����ʻ;����ӭ��������������ж������г�������ʱ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݵ�5�Ρ���6���˿��ղ�Ľ����2000�꣬2010���ҹ�ÿ10�����ܽ����̶ȵ�������£� 
����ͼ�е���Ϣ�����������գ�
��1��2010���ҹ����и����Ļ��̶ȵ��˿ڱ���Ϊ��
��2��2010���ҹ������Ļ��̶ȵ��˿���ࣻ
��3��ͬ2000����ȣ�2010���ҹ������Ļ��̶ȵ��˿��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�P������ΪC��1����2����
��1����˺����Ĺ�ϵʽ��
��2������C����x��ĶԳƵ�D��˳������A��C��B��D�������������ϴ��ڵ�E��ʹֱ��PE���ı���ACBD�ֳ������ȵ������ı��Σ����E�����ꣻ
��3���ڣ�2���������£����������Ƿ����һ��F��ʹ�á�PEF����PΪֱ�Ƕ����ֱ�������Σ������ڣ������F�����꼰��PEF��������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������MNPQ���ϵ׳�Ϊ2������Ϊ3��һ����Ϊ60�㣮������ABCD�ı߳�Ϊ1������һ��AD��MN�ϣ��Ҷ���A��M�غϣ��ֽ�������ABCD�����ε������ر�MN��NP��PQ���з�������������һ��������Q�غϼ�ֹͣ������
��1������������ͼ�У��ó߹滭����A������������������������������·��ͼ��
��2�������������������������е�A��������·��������MNPQ������MN��NP��PQ��Χ��ͼ�ε����S�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��F�ֱ���������ABCD�ı�BC��CD�ϵĵ㣬BE=CF������AE��BF������ABE�������ε����İ���ʱ�뷽����ת����BCF����ת��Ϊ���� 0�㣼����180�㣩����Ϧ�= �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com