
����Ŀ����֪������y��x2+��2n��1��x+n2��1��nΪ��������
��1�����������߾�������ԭ�㣬���Ҷ����ڵ�������ʱ�����������Ӧ�ĺ�����ϵʽ��
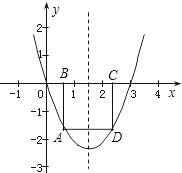
��2����A�ǣ�1����ȷ������������λ��x���·������ڶԳ�������һ�����㣬��A��x���ƽ���ߣ�������������һ��D������AB��x����B��DC��x����C��
����BC��1ʱ�������ABCD���ܳ���
�����ʾ���ABCD���ܳ��Ƿ�������ֵ��������ڣ������������ֵ����ָ����ʱA������꣮��������ڣ���˵�����ɣ�
���𰸡���1��y��x2��3x����2��������ABCD���ܳ�Ϊ6������x��![]() ʱ������ABCD���ܳ�C���ֵΪ
ʱ������ABCD���ܳ�C���ֵΪ![]() ����ʱ��A������ΪA��
����ʱ��A������ΪA��![]() ��
��![]() ����
����
��������
��1����ԭ��������������ߵĽ���ʽ�У��������n��ֵ��Ȼ����������߶����ڵ����������������nֵ��ȥ�����ɵó�����Ķ��κ�������ʽ��
��2�����ȸ��������ߵĽ���ʽ�����������x����һ����E�����꣬���������ߺ;��εĶԳ��Կ�֪��OB�ij�������OE��BC�IJ��һ�룬�ɴ˿����OB�ij�����B������꣬Ȼ����������ߵĽ���ʽ�м������B�������꣬Ҳ�͵ó��˾���AB�ߵij���������������ε��ܳ�����˼·ͬ�ٿ����A�����꣨������꣬���������ߵĽ���ʽ��ʾ�����꣩��Ҳ���ܱ�ʾ��B������꣬���ɵó�OB�ij���ͬ�ٿɵó�BC�ij�����AB�ij�����A��������ľ���ֵ���ɴ˿ɵó�һ�����ھ����ܳ���A��������ĺ�����ϵʽ�����ݶ��κ��������ʿɵó������ܳ������ֵ����Ӧ��A�����꣮
��1������֪��������n2��1��0
��������̣���n1��1��n2����1
��n��1ʱ����y��x2+x���������ߵĶ��㲻�ڵ������ޣ�
��n����1ʱ����y��x2��3x���������ߵĶ����ڵ������ޣ�
������ĺ�����ϵʽΪy��x2��3x��
��2����y��x2��3x��
��y��0����x2��3x��0��
���x1��0��x2��3
����������x�����һ������ΪE��3��0��
�����Ķ���Ϊ![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]() �������λ����ͼ��ʾ��
�������λ����ͼ��ʾ��
�١�BC��1����֪OB��![]() ����3��1����1��
����3��1����1��
��B��1��0��
���A�ĺ�����x��1���ֵ�A��������y��x2��3x�ϣ�
���A��������y��12��3��1����2��
��AB��|y|��|��2|��2��
�����ABCD���ܳ�Ϊ��2��AB+BC����2����2+1����6��
�ڡߵ�A��������y��x2��3x�ϣ��ʿ���A�������Ϊ��x��x2��3x����
��B���������x��0����![]()
��BC��3��2x��A��x���·���
��x2��3x��0��
��AB��|x2��3x|��3x��x2
�����ABCD���ܳ�C��2[��3x��x2��+��3��2x��]��![]() ��
��
��a����2��0�������߿������£����κ��������ֵ��
�൱x��![]() ʱ������ABCD���ܳ�C���ֵΪ
ʱ������ABCD���ܳ�C���ֵΪ![]() ��
��
��ʱ��A������ΪA![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
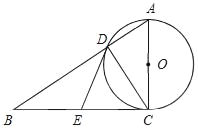
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬E��BC���е㣬��ACΪֱ������O��AB�߽��ڵ�D������DE��
(1)��֤��DE����O�����ߣ�
(2)��CD��6cm��DE��5cm������Oֱ���ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
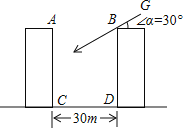
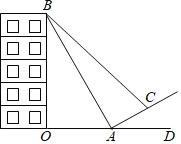
����Ŀ����������¥֮��ľ���CD=30�ף�¥AC��BD��Ϊ10�㣬ÿ��¥��3�ף�
��1������ijʱ�̣�̫������GB��ˮƽ��ļн�Ϊ30�����˿�B¥��Ӱ������A¥�ĵڼ��㣿
��2����̫��������ˮƽ��ļн�Ϊ���ٶ�ʱ��B¥��Ӱ�Ӹպ�����A¥�ĵײ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ǿ��ë������ƹ���������������������˶���ÿλͬѧ������ֻ��ѡ��һ�������˶����Ը�Уѧ�������ȡ![]() ���е��飬���ݵ�������������ͼ��������Ƶ���ֲ���������ͳ��ͼ��
���е��飬���ݵ�������������ͼ��������Ƶ���ֲ���������ͳ��ͼ��
�˶���Ŀ | Ƶ�� |
��� | 30 |
���� | a |
ƹ���� | 36 |
���� | b |
���� | 12 |
���������ͼ����Ϣ����������⣺
![]() Ƶ���ֲ����е�
Ƶ���ֲ����е�![]() ______��
______��![]() ______��
______��
![]() ������ͳ��ͼ�У������������ڵ����ε�Բ�Ľ�Ϊ______�ȣ�
������ͳ��ͼ�У������������ڵ����ε�Բ�Ľ�Ϊ______�ȣ�
![]() ȫУ�ж�����ѧ��ѡ��μ�ƹ�����˶���
ȫУ�ж�����ѧ��ѡ��μ�ƹ�����˶���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
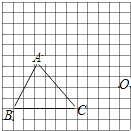
����Ŀ������ͼ�ķ���ֽ�У�ÿ��С����ı߳�����1����λ����һ��O�͡�ABC��
��1�����Ե�OΪλ�����ģ��ѡ�ABC��СΪԭ����һ�루���ı䷽���õ���A��B��C�䣻
��2�������ʵ��ķ�ʽ������A��B��C��Ķ���A�䡢B�䡢C���λ�ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽���꼶ѧ��˫���յĿ����Ķ������ѧУ��������˸��꼶25��ѧ�����õ���һ���������ݣ���ͳ�Ʊ����£�
���꼶25��ѧ��˫���տ����Ķ�ʱ��ͳ�Ʊ�
�Ķ�ʱ�� | 1Сʱ | 2Сʱ | 3Сʱ | 4Сʱ | 5Сʱ | 6Сʱ |
���� | 3 | 4 | 6 | 3 | 2 |
��1��������Ķ�ʱ��Ϊ4Сʱ��������ռ�ٷֱȣ�
��2����ȷ�����������������ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ѧ����ʵ��С��һ�λ�У�����һ��¥���ĸ߶ȣ���ͼ����ɽ���½�A���������¥����¥��B�������Ϊ60�㣬��ɽ�������ߵ�C���ٲ��B�������Ϊ45�㣬��֪ɽ�µ��±�i��1��![]() ��OA��200m����O��A��D��ͬһ��ֱ���ϣ�
��OA��200m����O��A��D��ͬһ��ֱ���ϣ�
(1)��¥��OB�ĸ߶ȣ�
(2)��ɽ����AC�ľ���(�����������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD�У�AB��4��BC��6����E��AB���ϣ���ֽƬ��CE�۵�����B���ڵ�F����EF��CF�ֱ�AD�ڵ�G��H����EG��GH����AE�ij�Ϊ( )
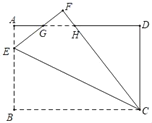
A. ![]() B. 1C.
B. 1C. ![]() D. 2
D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬������y��ax2��2ax��3a�ֱ�x����A��B���㣨��A�ڵ�B�IJࣩ����y�ύ�ڵ�C������AC��tan��ACO��![]() ��
��
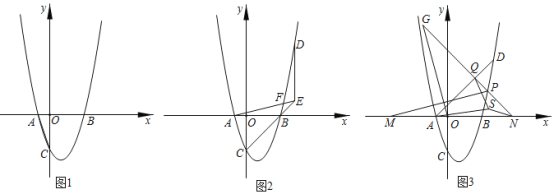
��1����ͼl����a��ֵ��
��2����ͼ2��D�ǵ�һ�����������ϵĵ㣬����D��y���ƽ���߽�CB���ӳ����ڵ�E������AE��BD�ڵ�F��AE��BD�����D�����ꣻ
��3����ͼ3���ڣ�2���������£�����AD��P�ǵ�һ�����������ϵĵ㣨��P���D���غϣ�������P��AD�Ĵ��ߣ�����ΪQ����x���ڵ�N����M��x���ϣ���M�ڵ�N����ࣩ����G��NP���ӳ����ϣ�MP��OG����MPN����MOG��45����MN��10![]() ����S����AQN��һ�㣬����AS��QS��NS��AS��AQ��QS��
����S����AQN��һ�㣬����AS��QS��NS��AS��AQ��QS��![]() SN����QS�ij���
SN����QS�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com