
【题目】已知:在平面直角坐标系中,O为坐标原点,抛物线y=ax2﹣2ax﹣3a分别交x轴于A、B两点(点A在点B的侧),与y轴交于点C,连接AC,tan∠ACO=![]() .
.
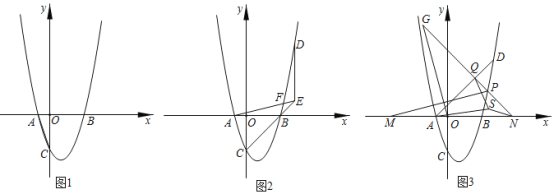
(1)如图l,求a的值;
(2)如图2,D是第一象限抛物线上的点,过点D作y轴的平行线交CB的延长线于点E,连接AE交BD于点F,AE=BD,求点D的坐标;
(3)如图3,在(2)的条件下,连接AD,P是第一象限抛物线上的点(点P与点D不重合),过点P作AD的垂线,垂足为Q,交x轴于点N,点M在x轴上(点M在点N的左侧),点G在NP的延长线上,MP=OG,∠MPN﹣∠MOG=45°,MN=10![]() .点S是△AQN内一点,连接AS、QS、NS,AS=AQ,QS=
.点S是△AQN内一点,连接AS、QS、NS,AS=AQ,QS=![]() SN,求QS的长.
SN,求QS的长.
【答案】(1) a=1; (2) D(4,5);(3) ![]()
【解析】
(1)由ax2-2ax-3a=0,可得到A(-1,0),B(3,0),OA=1,再根据条件tan∠ACO=![]() 可求得C(0,-3),即可求出a的值;
可求得C(0,-3),即可求出a的值;
(2)构造全等三角形Rt△ARE≌Rt△DRB,∴AR=DR,建立方程求解;
(3)过点G、P分别作x轴的垂线,垂足分别为K、H,构造全等三角形△MHP≌△GKO,利用特殊角45°构造等腰直角三角形,从而证得MK=HN=PH=KO,设点P(m,m2-2m-3),根据题目条件建立方程10![]() =m2-2m-3+m2-2m-3+m+m2-2m-3,可求得P(
=m2-2m-3+m2-2m-3+m+m2-2m-3,可求得P(![]() ,
,![]() );过点A作AT⊥QS,垂足为T,过点N作NZ⊥QS,垂足为Z,构造全等三角形△ATQ≌△QZN,运用勾股定理可求出QS.
);过点A作AT⊥QS,垂足为T,过点N作NZ⊥QS,垂足为Z,构造全等三角形△ATQ≌△QZN,运用勾股定理可求出QS.
解:(1)如图1,
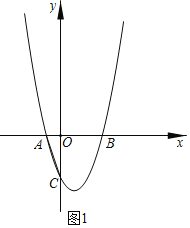
令y=0,则ax2﹣2ax﹣3a=0,
解得:x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),OA=1,
∵tan∠ACO=![]() ,∴OC=3,即C(0,﹣3),
,∴OC=3,即C(0,﹣3),
令x=0,y=﹣3a=﹣3,∴a=1
(2)如图2,延长DE交x轴于R,
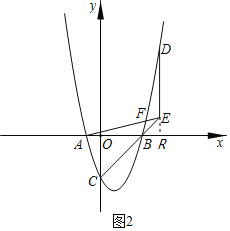
∵OC=OB=3,
∴∠OCB=∠OBC=45°,
∵DR∥y轴,
∴∠DER=∠OCB=45°,
∴∠RBE=∠REB=45°,
∴RB=RE,
∵AE=BD,
∴Rt△ARE≌Rt△DRB,
∴AR=DR,
设D(t,t2﹣2t﹣3),AR=t+1,DR=t2﹣2t﹣3,
∴t+1=t2﹣2t﹣3
解得:t1=4,t2=﹣1(舍去),
∴D(4,5).
(3)如图3,过点G、P分别作x轴的垂线,垂足分别为K、H,
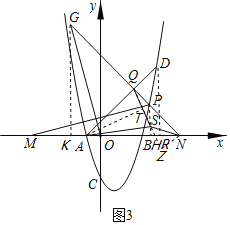
∵AR=DR=5,
∴∠RAD=45°,
∵NG⊥AD,
∴∠AQN=span>90°,
∴∠QAN=∠QNA=45°,
∵∠GKN=90°,
∴∠KGN=∠KNG=45°,
∴GK=KN,
∵∠PHN=90°,
∴∠HPN=∠HNP=45°,
∴HP=HN,
∵∠MPN﹣∠MOG=45°,
∴∠MPH=∠MOG,
∴∠MPH+∠HPN﹣∠MOG=45°,
∵MP=OG,∠MHP=∠GKO=90°,
∴△MHP≌△GKO,
∴MH=GK,PH=KO,
∵KN=GK,
∴MH=KN,
∴MK=HN=PH=KO,
设点P(m,m2﹣2m﹣3),
∵MN=MK+KO+OH+HN,
∴10![]() =m2﹣2m﹣3+m2﹣2m﹣3+m+m2﹣2m﹣3,
=m2﹣2m﹣3+m2﹣2m﹣3+m+m2﹣2m﹣3,
整理得:12m2﹣20m﹣77=0,
解得:m1=![]() ,m2=-
,m2=-![]() (舍去),
(舍去),
∴P(![]() ,
,![]() ),
),
ON=OH+HN=![]() ,AN=AO+ON=
,AN=AO+ON=![]() ,
,
在等腰直角三角形AQN中,由勾股定理可得QA=QN=![]() ,
,
过点A作AT⊥QS,垂足为T,过点N作NZ⊥QS,垂足为Z,
∵∠QAT+∠AQT=90°,∠NQZ+∠AQT=90°,
∴∠QAT=∠NQZ,
∵∠ATQ=∠QZN=90°,AQ=NQ,
∴△ATQ≌△QZN(AAS),
∴QT=ZN,AT=QZ,
∵AQ=AS,AT⊥QS,
∴QT=ST,
即QT=ZN=ST=![]() QS,
QS,
∵QS=![]() SN,
SN,
∴2NZ═![]() SN,sin∠ZSN=
SN,sin∠ZSN=![]() ,
,
∴∠ZSN=∠ZNS=45°,
∴ZN=ZS,
∴ZN=ZS=TS=TQ=![]() AT,
AT,
在Rt△ATQ中,由勾股定理可得QT=![]()
∴QS=2QT=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标![]() 系中,直线
系中,直线![]() 与坐标轴
与坐标轴![]() 轴交于点
轴交于点![]() 与
与![]() 轴交于点
轴交于点![]() 过
过![]() 两点的抛物线
两点的抛物线![]() ,点
,点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() 交抛物线于点
交抛物线于点![]() .
.
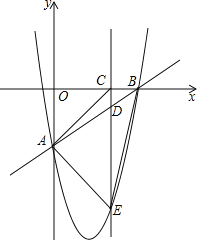
(1)求抛物线的解析式;
(2)当![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(3)是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2021年世界园艺博览会将在扬州枣林湾举办,有一块枣林湾博览会的直传牌CD竖立在路边,其中CB是支柱.小梅同学想计算出CD的长度.于是在A处测得支柱B处的俯角为30°.测得顶端D处的仰角为42°,同时测量出AB的长度是10m,BC的长度是6m.求宜传牌CD的长度(结果保留小数点后一位).(参考数据:![]() ≈1.73,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
≈1.73,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
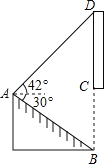
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.
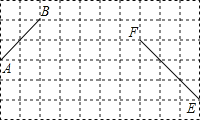
(1)在图中以AB为边画Rt△BAC,点C在小正方形的顶点上,使∠BAC=90°,tan∠ACB=![]() ;
;
(2)在(1)的条件下,在图中画以EF为边且面积为3的△DEF,点D在小正方形的顶点上,连接CD、BD,使△BDC是锐角等腰三角形,直接写出∠DBC的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.

(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为构建“魅力雨花,和谐雨花,人文雨花”,规划在圭塘河上修建一座观光人行桥(如图1),此工程由桥梁工程与桥上拱形工程组成,桥上拱形工程包含三组完全相同的拱形,观光人行桥的正规图如图2所示,已知桥面上三组拱桥都为相同的抛物线![]() 的一部分,拱高(抛物线最高点到桥面的距离)为16米,三条抛物线依次与桥面AB相较于点A,C,D,B.
的一部分,拱高(抛物线最高点到桥面的距离)为16米,三条抛物线依次与桥面AB相较于点A,C,D,B.

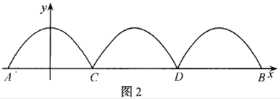
(1)求桥长AB;
(2)已知一组桥拱的造价为a万元,桥面每米的平均造价为b万元.若一组桥拱的造价为整个桥面造价的![]() ,这座观光桥的总造价为504万元,求a,b的值.
,这座观光桥的总造价为504万元,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全面推进“三供一业”分离移交工作,甲、乙两个工程队承揽了某社区2400米的电路管道铺设工程.已知甲队每天铺设管道的长度是乙队每天铺设管道长度的1.5倍,若两队各自独立完成1200米的铺设任务,则甲队比乙队少用10天.
(1)求甲、乙两工程队每天分别铺设电路管道多少米;
(2)若甲队参与该项工程的施工时间不得超过20天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线相交于O,给出下列 5个条件:①AB∥CD ;②AD∥BC;③AB=CD ;④∠BAD=∠BCD;⑤OA=OC.从以上5个条件中任选 2个条件为一组,能推出四边形ABCD为平行四边形的有( )
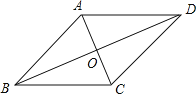
A. 4组 B. 5组 C. 6组 D. 7组
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com