
【题目】观察下列三行数,并完成后面的问题:
①﹣2,4,﹣8,16,﹣32,…;
②l,﹣2,4,﹣8,16,…;
③0,﹣3,3,﹣9,15,…
(1)思考第①行数的规律,写出第n个数字是多少(用含n的式子表示);
(2)第②行数和第①行数有什么关系?第③行数和第②行数又有什么关系?
(3)设x,y,z分别表示第①②③行数的第10个数字,求x+y+z的值.
【答案】(1)(﹣2)n;(2)第②行数是第①行数的﹣![]() 倍,第③行数比第②行对应数少1;(3)﹣1.
倍,第③行数比第②行对应数少1;(3)﹣1.
【解析】
(1)观察可看出第一行的数分别是-2的1次方,2次方,3次方,4次方…且偶数项是正数,奇数项是负数,用式子表示规律为:(-2)n;
(2)观察第②行数是第①行数的![]() 倍,计算出第③行数和第②行数的差,即可得出答案;
倍,计算出第③行数和第②行数的差,即可得出答案;
(3)分别求得第①②③行的第10个数,得出x,y,z代入求得答案即可.
(1)∵﹣2,4,﹣8,16,…;
∴第①行数是:(﹣2)1,(﹣2)2,(﹣2)3,(﹣2)4,…(﹣2)n;
故答案是:(﹣2)n;
(2)第②行数是第①行数的![]() 倍,
倍,
第③行数比第②行对应数少1;
(3)由题意:![]()
![]()
![]()
=1024﹣512﹣513=﹣1.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2). 
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求经过点C的反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集到的数据绘制成如下两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题.
学生上学方式扇形统计图

学生上学方式条形统计图
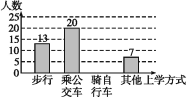
(1)m等于百分之多少,这次共抽取几名学生进行调查,并补全条形统计图.
(2)在这次抽样调查中,采用哪种上学方式的人数最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学骑自行车去郊外春游,骑行1小时后,自行车出现故障,维修好后继续骑行,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的图象.
(1)根据图象回答:小明到达离家最远的地方用了多长时间?此时离家多远?
(2)求小明出发2.5小时后离家多远;
(3)求小明出发多长时间离家12千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表: 我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
序号 | 1 | 2 | 3 | … |
图形 | x x | x x x | x x x x | … |
(1)第3格的“特征多项式”为 , 第4格的“特征多项式”为 , 第n格的“特征多项式”为;
(2)若第1格的“特征多项式”的值为﹣10,第2格的“特征多项式”的值为﹣16. ①求x,y的值;
②在①的条件下,第n格的“特征多项式”是否有最小值?若有,求出最小值和相应的n值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上. 
(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有甲、乙两个不透明的袋子,甲袋内装有标记数字﹣1,2,3的三张卡片,乙袋内装有标记数字2,3,4的三张卡片(卡片除数字不同其余都相同).先从甲袋中随机抽取一张卡片,记录下数字,再从乙袋中随机抽取一张卡片,记录下数字.
(1)利用列表或画树状图的方法(只选其中一种)表示出所抽两张卡片上数字之积所有可能的结果:
(2)求抽出的两张卡片上的数字之积是3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A(-2,0),B(4,0),现同时将点A、B分别向上平移4个单位,再向右平移2个单位,得到点A、B的对应点C、D,连接AC,CD、BD.
(1)直接写出点C、D的坐标,求四边形ABDC的面积;
(2)动点P从点C出发,以每秒1个单位的速度,沿射线CO运动.设点P运动时间为t秒.连结PA,设三角形AOP的面积为S ,求S与t之间的关系式;
(3)如图,在(2)的条件下,在线段BO上取一点E,使2BE=OB,连接PB、CE相交于点F,当三角形AOP的面积是四边形ABDC的![]() 时,求点F的坐标.
时,求点F的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com