
【题目】观察下表: 我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
序号 | 1 | 2 | 3 | … |
图形 | x x | x x x | x x x x | … |
(1)第3格的“特征多项式”为 , 第4格的“特征多项式”为 , 第n格的“特征多项式”为;
(2)若第1格的“特征多项式”的值为﹣10,第2格的“特征多项式”的值为﹣16. ①求x,y的值;
②在①的条件下,第n格的“特征多项式”是否有最小值?若有,求出最小值和相应的n值;若没有,请说明理由.
【答案】
(1)16x+9y;25x+16y;(n+1)2x+n2y
(2)解:①∵第1格的“特征多项式”的值为﹣8,第2格的“特征多项式”的值为﹣11,
∴根据题意可得: ![]() ,
,
解得: 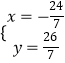 ;
;
②有最小值,
将x=﹣ ![]() ,y=
,y= ![]() 代入(n+1)2x+n2y=(﹣
代入(n+1)2x+n2y=(﹣ ![]() )(n+1)2+
)(n+1)2+ ![]() n2=
n2= ![]() (n﹣12)2﹣
(n﹣12)2﹣ ![]() ,
,
当n=12时,最小值为﹣ ![]()
【解析】解:(1)第3格的“特征多项式”为:16x+9y;第4格的“特征多项式”为:25x+16y; 第n格的“特征多项式”为:(n+1)2x+n2y;
故答案为:16x+9y;25x+16y;(n+1)2x+n2y;
(1)利用已知表格中x,y个数变化规律得出第2格的“特征多项式”以及第n格的“特征多项式”;(2)①利用(1)中所求得出关于x,y的等式组成方程组求出答案;②利用二次函数最值求法得出答案.


科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数: ![]() ,称为数列
,称为数列![]() .计算
.计算![]() ,
, ![]() ,
, ![]() 将这三个数的最小值称为数列
将这三个数的最小值称为数列![]() 的价值.例如,对于数列2,﹣1,3,因为
的价值.例如,对于数列2,﹣1,3,因为![]() ,
, ![]() ,
, ![]() ,所以数列2,﹣1,3的价值为
,所以数列2,﹣1,3的价值为![]() .
.
小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列﹣1,2,3的价值为![]() ;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列﹣4,﹣3,2的价值为 ;
(2)将“﹣4,﹣3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为 ,取得价值最小值的数列为 (写出一个即可);
(3)将2,﹣9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两公司近年销售收入情况的折线统计图,根据统计图得出下列结论,其中正确的是( )
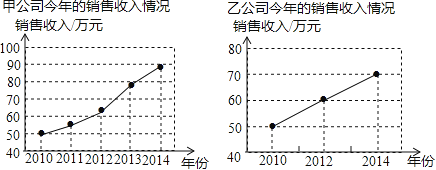
A.甲公司近年的销售收入增长速度比乙公司快
B.乙公司近年的销售收入增长速度比甲公司快
C.甲、乙两公司近年的销售收入增长速度一样快
D.不能确定甲、乙两公司近年销售收入增长速度的快慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小刘离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示,则下列说法不正确的是( )
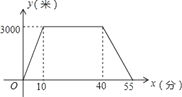
A. 小刘家与超市相距3000米 B. 小刘去超市途中的速度是300米/分
C. 小刘在超市逗留了30分钟 D. 小刘从超市返回家比从家里去超市的速度快
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC= ![]() .
. 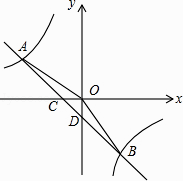
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数,并完成后面的问题:
①﹣2,4,﹣8,16,﹣32,…;
②l,﹣2,4,﹣8,16,…;
③0,﹣3,3,﹣9,15,…
(1)思考第①行数的规律,写出第n个数字是多少(用含n的式子表示);
(2)第②行数和第①行数有什么关系?第③行数和第②行数又有什么关系?
(3)设x,y,z分别表示第①②③行数的第10个数字,求x+y+z的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
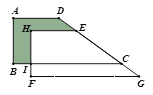
【题目】如图所示,直角梯形ABCD 沿直线DC方向平移可得直角梯形HFGE,如果AB=4,BC=9,BI=1.2,HI=3那么阴影面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名学生中选拨一人参加射击比赛,对他们的射击水平进行了测验,两人在相同条件下各射靶6次,命中的环数如下:
甲:7,8,6,10,10,7
乙:7, 7,8,8,10,8,
如果你是教练你会选拨谁参加比赛?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
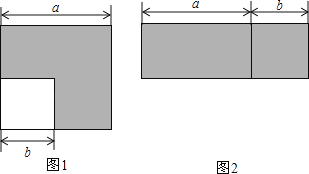
【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个正方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com