
【题目】小亮妈妈下岗后开了一家糕点店,现有10.2千克面粉,10.2千克鸡蛋,计划加工一般糕点和精制糕点两种产品共50盒.

⑴有哪几种符合题意的加工方案?请你帮忙设计出来;
⑵若销售一般糕点和精制糕点的利润分别为1.5元/盒和2元/盒,试问哪种方案使小亮妈妈可获得最大利润?最大利润是多少?
【答案】(1)加工方案有三种:
①加工一般糕点24盒、精制糕点26盒;
②加工一般糕点25盒、精制糕点25盒;
③加工一般糕点26盒、精制糕点24盒.
(2) 加工一般糕点24盒、精制糕点26盒时,可获得最大利润.最大利润为=88元.
【解析】
(1)本题可根据“加工一般糕点用的面粉的量+加工精制糕点用的面粉的量≤10.2”来列出不等式组,求出自变量的取值范围,判断出符合条件的方案;
(2)根据一盒一般糕点和精制糕点的利润,我们可看出,制作的精制糕点越多,利润越大,因此找出(1)中精制糕点最多的方案,计算出这个方案的利润即可.
解:(1)设加工一般糕点x盒,则加工精制糕点(50-x)盒,根据题意得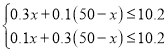
解这个不等式组,得24≤x≤26
因为x为整数,所以x=24,25,26.
因此,加工方案有三种:
①加工一般糕点24盒、精制糕点26盒;
②加工一般糕点25盒、精制糕点25盒;
③加工一般糕点26盒、精制糕点24盒.
(2)由题意知,显然精制糕点数越多利润越大,故当加工一般糕点24盒、精制糕点26盒时,可获得最大利润.
最大利润为24×1.5+26×2=88(元).
答:加工一般糕点24盒、精制糕点26盒时,可获得最大利润.最大利润为=88元.


科目:初中数学 来源: 题型:
【题目】为提升青少年的身体素质,郑州市在全市中小学推行“阳光体育”活动,河南省实验中学为满足学生的需求,准备再购买一些篮球和足球.如果分别用800元购买篮球和足球,购买篮球的个数比足球的个数少2个,足球的单价为篮球单价的![]() .
.
(1)求篮球、足球的单价分别为多少元?
(2)学校计划用不多于5200元购买篮球、足球共60个,那么至少购买多少个足球?
(3)在(2)的条件下,若篮球数量不能低过15个,那么有多少种购买方案?哪种方案费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB∥CD,点E是直线AB、CD之间的一点,连接EA、EC.
(1)探究猜想:
①若∠A=20°,∠C=50°,则∠AEC= .
②若∠A=25°,∠C=40°,则∠AEC= .
③猜想图1中∠EAB、∠ECD、∠AEC的关系,并证明你的结论(提示:作EF∥AB).
(2)拓展应用:
如图2,AB∥CD,线段MN把ABCD这个封闭区域分为I、Ⅱ两部分(不含边界),点E是位于这两个区域内的任意一点,请直接写出∠EMB、∠END、∠MEN的关系.
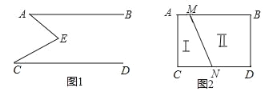
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,D为AB的中点,点P在线段上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,点P和点Q是直线BD上不重合的两个动点,AP∥CQ,AD=BD.
(1)如图①,求证:BP+BQ=BC;
(2)请直接写出图②,图③中BP、BQ、BC三者之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若DQ=2,DP=6,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 平行线
平行线![]() 与
与![]() 与
与![]() 与
与![]() 之间的距离分别为
之间的距离分别为![]() 且
且![]()
![]() ,
,![]() .我们把四个顶点分别在
.我们把四个顶点分别在![]() 这四条平行线上的四边形称为“线上四边形”
这四条平行线上的四边形称为“线上四边形”
(1)如图1,正方形![]() 为“线上四边形”,
为“线上四边形”,![]() 于点
于点![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .求正方形
.求正方形![]() 的边长.
的边长.

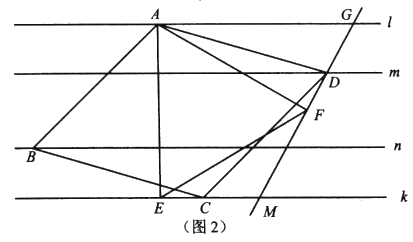
(2)如图2,菱形![]() 为“线上四边形”且
为“线上四边形”且![]() 是等边三角形,点
是等边三角形,点![]() 在直线
在直线![]() 上,连接
上,连接![]() 且
且![]() 的延长线分别交直线
的延长线分别交直线![]() 于点
于点![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
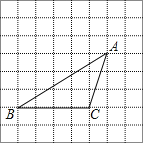
【题目】如图,将方格纸中的三角形ABC先向右平移2格得到三角形DEF,再将三角形DEF向上平移3格得到三角形GPH.
(1)动手操作:按上面步骤作出经过两次平移后分别得到的三角形;
(2)设AC与DE相交于点M,则图中与∠BAC相等的角有 个;
(3)若∠BAC=43°,∠B=32°,则∠PHG= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
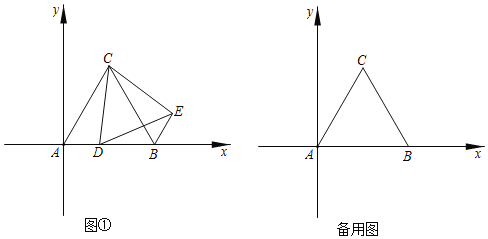
【题目】如图,在平面直角坐标系中,等边△ABC的顶点A,B的坐标分别为(0,0),(6,0),点D是x轴上的一个动点,连接CD,将△ACD绕点C逆时针旋转60°得到△BCE,连接DE.
(1)点C的坐标为____,△CDE为____三角形;
(2)当点D在线段AB上运动时,四边形CDBE的周长是否存在最小值?若存在,求出四边形CDBE的周长最小值及此时点D的坐标;若不存在,请说明理由;
(3)当△BDE是直角三角形时,请直接写出点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com