练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，某翼装飞行员从离水平地面高AC=500m的A处出发，沿着俯角为15°的方向，直线滑行1600米到达D点，然后打开降落伞以75°的俯角降落到地面上的B点．求他飞行的水平距离BC（结果精确到1m）．

    【答案】1575米.

    【解析】如图，过点D作DE⊥AC，作DF⊥BC，垂足分别为E，F，

    ∵AC⊥BC，∴四边形ECFD是矩形，

    ∴EC＝DF．

    在Rt△ADE中，∠ADE＝15°，AD＝1600．

    ∴AE＝AD·sin∠ADE＝1600sin15°，

    DE＝AD·cos∠ADE＝1600cos15°，

    ∵EC＝AC－AE，∴EC＝500－1600sin15°．

    在Rt△DBF中，BF＝DF·tan∠FDB＝ECtan15°，

    ∴BC＝CF＋BF＝1600cos15°＋（500－1600sin15°）·tan15°≈1575．

    ∴运动员飞行的水平距离约为1575米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（操作发现）如图1，为等腰直角三角形，，先将三角板的角与重合，再将三角板绕点按顺时针方向旋转（旋转角大于且小于），旋转后三角板的一直角边与交于点．在三角板另一直角边上取一点，使，线段上取点，使，连接，．

    （1）请求出的度数？

    （2）与相等吗？请说明理由；

    （类比探究）如图2，为等边三角形，先将三角板中的角与重合，再将三角板绕点按顺时针方向旋转（旋转角大于且小于）.旋转后三角板的一直角边与交于点.在三角板斜边上取一点，使，线段上取点，使，连接，.

    （3）直接写出_________度；

    （4）若，，求线段的长度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（　　）

    A. 4B. 3C. 2D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC面积为1，第一次操作：分别延长AB，BC，CA至点A1，B1，C1，使A1B=AB，CB1=CB，C1A=CA，顺次连接A1，B1，C1，得到△A1B1C1．第二次操作：分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连接A2，B2，C2，得到△A2B2C2，…按此规律，要使得到的三角形的面积超过100，最少经过（　　）次操作．

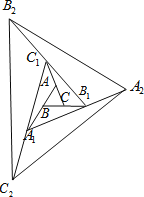
    A.3B.4C.5D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小亮妈妈下岗后开了一家糕点店，现有10.2千克面粉，10.2千克鸡蛋，计划加工一般糕点和精制糕点两种产品共50盒．

    ⑴有哪几种符合题意的加工方案？请你帮忙设计出来；

    ⑵若销售一般糕点和精制糕点的利润分别为1.5元/盒和2元/盒，试问哪种方案使小亮妈妈可获得最大利润？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本题8分）△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．

    （1）按要求作图：

    ①画出△ABC关于原点O的中心对称图形△A1B1C1；

    ②画出将△ABC绕点A逆时针旋转90°得到△AB2C2，

    （2）回答下列问题：

    ①△A1B1C1中顶点A1坐标为 ；②若P（a，b）为△ABC边上一点，则按照（1）中①作图，点P对应的点P1的坐标为 ．

    【答案】（1）作图见解析；（2）（1，-2）（-a,-b）

    【解析】试题分析：（1）首先找出对应点的位置，再顺次连接即可；

    （2）①根据图形可直接写出坐标；②根据关于原点对称点的坐标特点可得答案．

    试题解析：（1）如图所示：

    （2）①根据图形可得A1坐标为（2，﹣4）；

    ②点P1的坐标为（﹣a，﹣b）．

    故答案为：（﹣2，﹣4）；（﹣a，﹣b）．

    考点：作图-旋转变换．

    【题型】填空题
    【结束】
    23

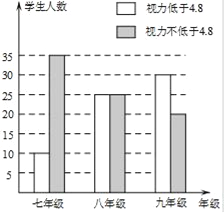
    【题目】在学习了“普查与抽样调查”之后，某校八（1）班数学兴趣小组对该校学生的视力情况进行了抽样调查，并画出了如图所示的条形统计图．请根据图中信息解决下列问题：

    （1）本次抽查活动中共抽查了　　名学生；

    （2）已知该校七年级、八年级、九年级学生数分别为360人、400人、540人．

    ①试估算：该校九年级视力不低于4.8的学生约有　　名；

    ②请你帮忙估算出该校视力低于4.8的学生数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是半圆半径，半径OC⊥AB于点O，点D是弧BC的中点，连接CD、AD、OD，给出以下四个结论：①∠DOB=∠ADC；②CE=OE；③△ODE∽△ADO；④2CD2=CE·AB．其中正确结论的序号是（　　）

    A. ①③ B. ②④ C. ①④ D. ①②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司分两次采购甲、乙两种商品，具体情况如下：

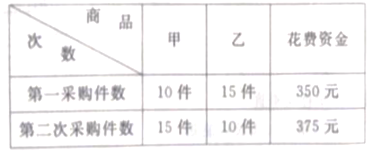
    （1）求甲、乙商品每件各多少元？

    （2）公司计划第三次采购甲、乙两种商品共31件，要求花费资金不超过475元，问最多可购买甲商品多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题正确的是（ ）

    A.一组对边平行，另一组对边相等的四边形是平行四边形

    B.两条对角线相等且有一个角是直角的四边形是矩形

    C.平行四边形两条对角线的平方和等于四条边的平方和

    D.有一条对角线平分一组对角的四边形是菱形

    查看答案和解析>>

    同步练习册答案