
【题目】某公司分两次采购甲、乙两种商品,具体情况如下:
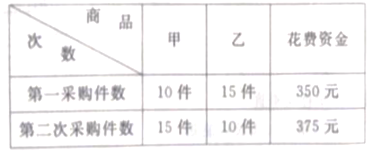
(1)求甲、乙商品每件各多少元?
(2)公司计划第三次采购甲、乙两种商品共31件,要求花费资金不超过475元,问最多可购买甲商品多少件?
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
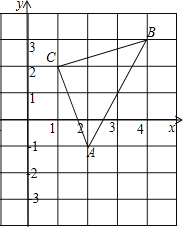
(1)写出点A、B的坐标:A( , )、B( , );
(2)求△ABC的面积;
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,画出△A′B′C′,写出A′、B′、C′三个点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为1.第一次操:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.

A.6B.5C.4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将方格纸中的三角形ABC先向右平移2格得到三角形DEF,再将三角形DEF向上平移3格得到三角形GPH.
(1)动手操作:按上面步骤作出经过两次平移后分别得到的三角形;
(2)设AC与DE相交于点M,则图中与∠BAC相等的角有 个;
(3)若∠BAC=43°,∠B=32°,则∠PHG= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
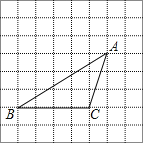
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶A,B,C在小正方形的顶点上,利用网格作图:
(1)将△ABC水平向右平移4个单位得到△A1B1C1,画出△A1B1C1.
(2)过AB的中点D作DE∥BC交AC于点E;
(3)求出△ABC 的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图是一次函数的图象,请根据图象回答下列问题:
(1)当x_____时,y>8;
(2)当-2≤x≤0时,则相应y的取值范围是______;
(3)如果这个函数y的值满足0≤y≤4,则相应的x的取值范围是______;
(4)根据图象求出一次函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
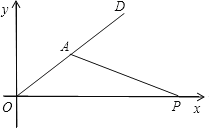
【题目】随着科学技术的发展,机器人早已能按照设计的指令完成各种动作.在坐标平面上,根据指令[S,α](S≥0,0°<α<180°)机器人能完成下列动作:先原地顺时针旋转角度α,再朝其对面方向沿直线行走距离s.
(1)填空:如图,若机器人在直角坐标系的原点,且面对y轴的正方向,现要使其移动到点A(2,2),则给机器人发出的指令应是 ;
(2)机器人在完成上述指令后,发现在P(6,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能截住小球.
(参考数据:sin53°≈0.8,cos37°≈0.80,tan37°≈0.75,tan26.5°≈0.5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com