
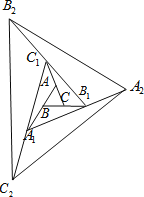
����Ŀ����ͼ����ABC���Ϊ1����һ�β������ֱ��ӳ�AB��BC��CA����A1��B1��C1��ʹA1B=AB��CB1=CB��C1A=CA��˳������A1��B1��C1���õ���A1B1C1���ڶ��β������ֱ��ӳ�A1B1��B1C1��C1A1����A2��B2��C2��ʹA2B1=A1B1��B2C1=B1C1��C2A1=C1A1��˳������A2��B2��C2���õ���A2B2C2�������˹��ɣ�Ҫʹ�õ��������ε��������100�����پ������������β�����
A.3B.4C.5D.6
���𰸡�A
��������
�ȸ�����֪���������A1B1C1����A2B2C2��������ٸ����������εı�����ϵ��⼴�ɣ�
�⣺��ABC���A1BB1����ȣ�AB=A1B������Ϊ1��2��BB1=2BC�����������Ϊ1��2��
�ߡ�ABC���Ϊ1��
��S��A1B1B=2��
ͬ���ɵã�S��C1B1C=2��S��AA1C=2��
��S��A1B1C1=S��C1B1C+S��AA1C+S��A1B1B+S��ABC=2+2+2+1=7��
ͬ����֤��A2B2C2�����=7����A1B1C1�����=49��
�����β���������Ϊ7��49=343��
�ʰ��˹��ɣ�Ҫʹ�õ��������ε��������100�����پ���3�β�����
��ѡ��A��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A����4��2����B��n����4��������һ�κ���y=kx+b�ͷ���������y=![]() ͼ����������㣮
ͼ����������㣮
��1����һ�κ����ͷ����������Ľ���ʽ��
��2������AOB�������
��3���۲�ͼ��ֱ��д������ʽkx+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵ�У���ABC�Ķ��㶼��������ϣ����У�C������Ϊ��1��2����
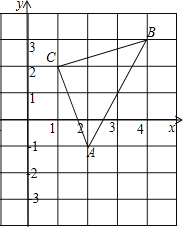
��1��д����A��B�����꣺A�� �� ����B�� �� ����
��2������ABC�������
��3������ABC������ƽ��2����λ���ȣ�������ƽ��1����λ���ȣ��õ���A��B��C�䣬������A��B��C�䣬д��A�䡢B�䡢C�����������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.Ϊ���˽�ij��ѧ![]() ��ѧ����������������������ȡ��
��ѧ����������������������ȡ��![]() ��ѧ�����е��飬�ڴ˴ε����У���������Ϊ
��ѧ�����е��飬�ڴ˴ε����У���������Ϊ![]() ��ѧ��������
��ѧ��������
B.��һ����Ϸ���н�����![]() ������
������![]() ����������Ϸһ�����н�
����������Ϸһ�����н�
C.�˽�������ÿ��������˿��������ó������鷽ʽ
D.����һöӲ�ң����泯�����DZ�Ȼ�¼�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���B����C��AB��10 cm��BC��8 cm��DΪAB���е㣬��P���߶�����3 cm/s���ٶ��ɵ�B���C�˶���ͬʱ����Q���߶�CA������ͬ�ٶ��ɵ�C���A�˶���һ���㵽���յ����һ����Ҳֹͣ�˶�������BPD���CQPȫ��ʱ�����P�˶���ʱ�䣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��.��ͼ�٣�ABC�У���BAC��ƽ����AB1�۵��������ص����֣������²�����B1A1C��ƽ����A1B2�۵��������ص����֣����������²�����BnAnC��nΪ����������ƽ����AnBn1�۵�����Bn���C�غϣ������۵����ٴΣ�ֻҪ���һ�ε�Bn���Cǡ���غϣ����Ǿͳ�BAC��ABC�ĺýǣ�
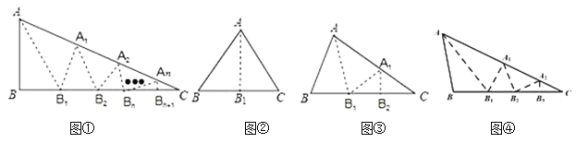
С��չʾ��ȷ��BAC��ABC�ĺýǵ��������Σ�
����һ����ͼ�ڣ��ص���������ABC����BAC��ƽ����AB1�۵�����B���C�غϣ�
���ζ�����ͼ�ۣ���ABC��BAC��ƽ����AB1�۵�,�����ص����֣������µIJ�����B1A1C��ƽ����A1B2�۵�����ʱ��B1���C�غϣ�
��̽�����֣�
����ͼ�ۣ�ABC�У�B2C�����������۵���BAC�Dz���ABC�ĺýǣ� �����������������������
�ƹ��ɲ��룺��i����ͼ�ܣ�С�����������۵�������BAC��ABC�ĺýǣ���̽��B��C��BC��֮��ĵ�����ϵ����˵�����ɣ�
��ii�������������ݲ��룺������n��nΪ�����������۵�BAC��ABC�ĺýǣ���B��C��BC��֮��ĵ�����ϵΪ ����ֱ��д�����ۣ�
��С���ҵ�һ�������Σ������Ƿֱ�Ϊ15,60,105������60��105�������Ƕ��Ǵ������εĺýǣ�������ɣ����һ�������ε���С����10����������������������ǵĶ�����ʹ�������ε������Ǿ��Ǵ������εĺýǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��װ����Ա����ˮƽ�����AC=500m��A�����������Ÿ���Ϊ15���ķ���ֱ����1600����D�㣬Ȼ�����ɡ��75���ĸ��ǽ��䵽�����ϵ�B�㣮�������е�ˮƽ����BC�������ȷ��1m����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�����Ϊ1����һ�β٣��ֱ��ӳ�AB��BC��CA����A1��B1��C1��ʹA1B��AB��B1C��BC��C1A��CA��˳������A1��B1��C1���õ���A1B1C1���ڶ��β������ֱ��ӳ�A1B1��B1C1��C1A1����A2��B2��C2��ʹA2B1��A1B1��B2C1��B1C1��C2A1��C1A1��˳������A2��B2��C2���õ���A2B2C2�������˹��ɣ�Ҫʹ�õ��������ε��������2016�����پ������������β�����

A.6B.5C.4D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��һ�κ�����ͼ�������ͼ��ش��������⣺
��1����x_____ʱ��y��8��
��2������2��x��0ʱ������Ӧy��ȡֵ��Χ��______��
��3������������y��ֵ����0��y��4������Ӧ��x��ȡֵ��Χ��______��
��4������ͼ�����һ�κ�����ϵʽ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com