
【题目】.如图①,ABC中,沿BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿B1A1C的平分线A1B2折叠,剪掉重叠部分;……将余下部分沿BnAnC(n为正整数)的平分线AnBn1折叠,点Bn与点C重合.无论折叠多少次,只要最后一次点Bn与点C恰好重合,我们就称BAC是ABC的好角.
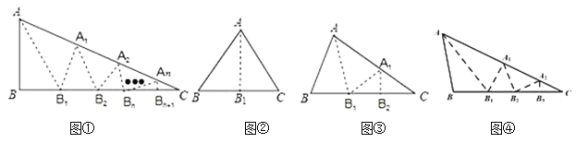
小丽展示了确定BAC是ABC的好角的两种情形.
情形一:如图②,沿等腰三角形ABC顶角BAC是平分线AB1折叠,点B与点C重合;
情形二:如图③,沿ABC的BAC的平分线AB1折叠,剪掉重叠部分;将余下的部分沿B1A1C的平分线A1B2折叠,此时点B1与点C重合.
(探究发现)
⑴如图③,ABC中,B2C,经过两次折叠,BAC是不是ABC的好角? .(填:“是”或“不是”)
⑵归纳猜想:(i)如图④,小丽经过三次折叠发现了BAC是ABC的好角,请探究B与C(BC)之间的等量关系,并说明理由.
(ii)根据以上内容猜想:若经过n(n为正整数)次折叠BAC是ABC的好角,则B与C(BC)之间的等量关系为 .(直接写出结论)
⑶小丽找到一个三角形,三个角分别为15,60,105,发现60和105的两个角都是此三角形的好角,请你完成,如果一个三角形的最小角是10,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.
【答案】(1)是;
(2)∠B=3∠C;∠B=n∠C;
(3)60°,105°;
(4)10°,160°.
【解析】
(1)仔细分析题意根据折叠的性质及“好角”的定义即可作出判断;
(2)因为经过三次折叠∠BAC是△ABC的好角,所以第三次折叠的∠A2B2C=∠C,由∠ABB1=∠AA1B1,∠AA1B1=∠A1B1C+∠C,又∠A1B1C=∠A1A2B2,∠A1A2B2=∠A2B2C+∠C,∠ABB1=∠A1B1C+∠C=∠A2B2C+∠C+∠C=3∠C,由此即可求得结果;
(3)根据好角的定义即可得出结果;
(4)根据好角的定义进行推理计算,即可得出结果.
解:(1)△ABC中,∠B=2∠C,经过两次折叠,∠BAC是△ABC的好角;
理由如下:小丽展示的情形二中,
∵沿∠BAC的平分线AB1折叠,
∴∠B=∠AA1B1;
又∵将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合,
∴∠A1B1C=∠C;
∵∠AA1B1=∠C+∠A1B1C(外角定理),
∴∠B=2∠C;
故答案为:是;
(2)∠B=3∠C;
在△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分,将余下部分沿∠B2A2C的平分线A2B3折叠,点B2与点C重合,则∠BAC是△ABC的好角.
理由如下:∵根据折叠的性质知,∠B=∠AA1B1,∠C=∠A2B2C,∠A1B1C=∠A1A2B2,
∴根据三角形的外角定理知,∠A1A2B2=∠C+∠A2B2C=2∠C;
∵根据四边形的外角定理知,∠BAC+∠B+∠AA1B1-∠A1B1C=∠BAC+2∠B-2C=180°,
根据三角形ABC的内角和定理知,∠BAC+∠B+∠C=180°,
∴∠B=3∠C;
由小丽展示的情形一知,当∠B=∠C时,∠BAC是△ABC的好角;
由小丽展示的情形二知,当∠B=2∠C时,∠BAC是△ABC的好角;
由小丽展示的情形三知,当∠B=3∠C时,∠BAC是△ABC的好角;
故若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为∠B=n∠C;
故答案为:∠B=3∠C;∠B=n∠C;
(3)由前边可以知道∠B和∠C有倍数关系,∠A是好角
所以60°=4×15°,60和15有倍数关系,105°应该是好角
105°=7×15°,105和15有倍数关系,60°应该是好角
故答案为:60°,105°;
(4)10°,160°;由(2)知,∠B=n∠C,∠BAC是△ABC的好角,
因为最小角是10°是△ABC的好角,
根据好角定义,则可设另两角分别为10m°,10mn°(其中m、n都是正整数).
由题意,得10m+10mn+10=180,所以m(n+1)=17.
因为m、n都是正整数,所以m与n+1是17的整数因子,
因此有:m=1,n+1=17;
所以m=1,n=16;
所以10m=10°,10mn=160°;
所以该三角形的另外两个角的度数分别为:10°,160°;
故答案为:10°,160°.


科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“奇特数”.例如:![]() ,
,![]() ,
,![]() ;则8、16、24这三个数都是奇特数.
;则8、16、24这三个数都是奇特数.

(1)填空:32___________奇特数,2018_________奇特数.(填“是”或者“不是”)
(2)设两个连续奇数是![]() 和
和![]() (其中
(其中![]() 取正整数),由这两个连续奇数构造的奇特数是8的倍数吗?为什么?
取正整数),由这两个连续奇数构造的奇特数是8的倍数吗?为什么?
(3)如图所示,拼叠的正方形边长是从1开始的连续奇数…,按此规律拼叠到正方形![]() ,其边长为403,求阴影部分的面积.
,其边长为403,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.

(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为2.4米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.2米,看台最低点A与旗杆底端D之间的距离为15米(C,A,D在同一条直线上).
(1)求看台最低点A到最高点B的坡面距离AB;
(2)一面红旗挂在旗杆上,固定红旗的上下两个挂钩G、H之间的距离为1.2米,下端挂钩H与地面的距离为1米,要求用30秒的时间将红旗升到旗杆的顶端,求红旗升起的平均速度(计算结果保留两位小数)(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,CB1=CB,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过100,最少经过( )次操作.
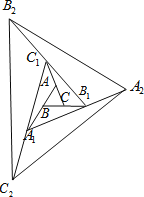
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点A逆时针旋转90°得到△AB2C2,
(2)回答下列问题:
①△A1B1C1中顶点A1坐标为 ;②若P(a,b)为△ABC边上一点,则按照(1)中①作图,点P对应的点P1的坐标为 .

【答案】(1)作图见解析;(2)(1,-2)(-a,-b)
【解析】试题分析:(1)首先找出对应点的位置,再顺次连接即可;
(2)①根据图形可直接写出坐标;②根据关于原点对称点的坐标特点可得答案.
试题解析:(1)如图所示:
(2)①根据图形可得A1坐标为(2,﹣4);
②点P1的坐标为(﹣a,﹣b).
故答案为:(﹣2,﹣4);(﹣a,﹣b).

考点:作图-旋转变换.
【题型】填空题
【结束】
23
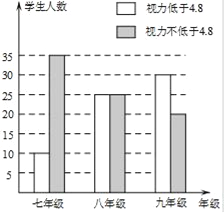
【题目】在学习了“普查与抽样调查”之后,某校八(1)班数学兴趣小组对该校学生的视力情况进行了抽样调查,并画出了如图所示的条形统计图.请根据图中信息解决下列问题:
(1)本次抽查活动中共抽查了 名学生;
(2)已知该校七年级、八年级、九年级学生数分别为360人、400人、540人.
①试估算:该校九年级视力不低于4.8的学生约有 名;
②请你帮忙估算出该校视力低于4.8的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月12日是我国第十个全国防灾减灾日,也是汶川地震十周年.为了弘扬防灾减灾文化,普及防灾减灾知识和技能,郑州W中学通过学校安全教育平台号召全校学生进行学习,并对学生学习成果进行了随机抽取,现对部分学生成绩(x为整数,满分100分)进行统计.绘制了如图尚不完整的统计图表:
调查结果统计表
组别 | 分数段 | 频数 |
A | 50≤x<60 | a |
B | 60≤x<70 | 80 |
C | 70≤x<80 | 100 |
D | 80≤x<90 | 150 |
E | 90≤x<100 | 120 |
合计 | b |
根据以上信息解答下列问题:
(1)填空:a= ,b= ;
(2)扇形统计图中,m的值为 ,“D”所对应的圆心角的度数是 度;
(3)本次调查测试成绩的中位数落在 组内;
(4)若参加学习的同学共有2000人,请你估计成绩在90分及以上的同学大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设超市购进这批水果的总量为m千克,每千克进价为n元(不计超市其它费用).
(1)如果超市在进价的基础上提高10%作为售价,此时:
①超市最终的销售额为_________元(用含m、n的代数式表示);
②在这一次销售中,超市_______(填:盈利或亏本).
(2)如果超市至少要获得17%的利润,请通过计算说明这种水果的售价最低应提高百分之几?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com