
【题目】如图,在四边形![]() 中,点
中,点![]() 分别是线段
分别是线段![]() 的中点,
的中点,![]() 分别是线段
分别是线段![]() 的中点,当四边形
的中点,当四边形![]() 的边满足___________________时,四边形
的边满足___________________时,四边形![]() 是菱形.
是菱形.

【答案】AB=CD
【解析】
本题可根据菱形的定义来求解.E、G分别是AD,BD的中点,那么EG就是△ADB的中位线,同理,HF是△ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG∥HF,EG=HF,因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=![]() CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
解:当AB=CD时,四边形EGFH是菱形.
∵点E,G分别是AD,BD的中点,
∴EG∥AB,同理HF∥AB,∴EG∥HF,EG=HF=![]() AB,
AB,
∴四边形EGFH是平行四边形.
∵EG=![]() AB,又可同理证得EH=
AB,又可同理证得EH=![]() CD,
CD,
∵AB=CD,
∴EG=EH,
∴四边形EGFH是菱形.
故答案为AB=CD.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1) 请你判断DA与CE的位置关系,并说明理由;
(2) 若DA平分∠BDC,CE⊥AE于点E,∠1=70°,试求∠FAB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的网格中,有一格点三角形ABC.(说明:顶点都在网格线交点处的三角形叫做格点三角形)

(1)将△ABC绕点C旋转180°,得到△A′B′C,请直接画出旋转后的△A′B′C.(友情提醒:别忘了标上相应的字母!)
(2)在网格中以AB为一边作格点△ABD(顶点在小正方形的顶点处的三角形称为格点三角形),使它的面积是△ABC的2倍,则点D的个数有个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图①,ABC中,沿BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿B1A1C的平分线A1B2折叠,剪掉重叠部分;……将余下部分沿BnAnC(n为正整数)的平分线AnBn1折叠,点Bn与点C重合.无论折叠多少次,只要最后一次点Bn与点C恰好重合,我们就称BAC是ABC的好角.
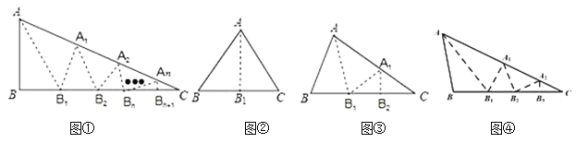
小丽展示了确定BAC是ABC的好角的两种情形.
情形一:如图②,沿等腰三角形ABC顶角BAC是平分线AB1折叠,点B与点C重合;
情形二:如图③,沿ABC的BAC的平分线AB1折叠,剪掉重叠部分;将余下的部分沿B1A1C的平分线A1B2折叠,此时点B1与点C重合.
(探究发现)
⑴如图③,ABC中,B2C,经过两次折叠,BAC是不是ABC的好角? .(填:“是”或“不是”)
⑵归纳猜想:(i)如图④,小丽经过三次折叠发现了BAC是ABC的好角,请探究B与C(BC)之间的等量关系,并说明理由.
(ii)根据以上内容猜想:若经过n(n为正整数)次折叠BAC是ABC的好角,则B与C(BC)之间的等量关系为 .(直接写出结论)
⑶小丽找到一个三角形,三个角分别为15,60,105,发现60和105的两个角都是此三角形的好角,请你完成,如果一个三角形的最小角是10,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组成员张广益对本年级期中考试数学成绩(成绩取整数,满分为100分)做了统计分析,绘制成如下频数、频率分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:
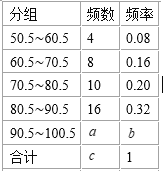
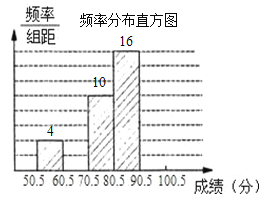
⑴填充频率分布表中的空格:a ,b ,c ;
⑵补全频率分布直方图;
⑶已知本年级共计1700名学生,若竞赛成绩在90分以上(不含90分)为优秀,估算本年级数学成绩优秀的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是BC边的中点,连接DE并延长交AB的延长线于点F,则在题中条件下,下列结论不能成立的是( )
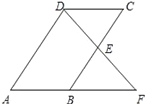
A. BE=CE B. AB=BF C. DE=BE D. AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请在图中作出△A′B′C′;(2)写出点A′、B′、C′的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com