
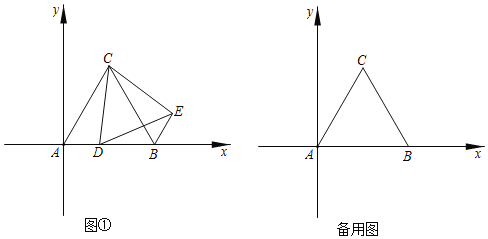
【题目】如图,在平面直角坐标系中,等边△ABC的顶点A,B的坐标分别为(0,0),(6,0),点D是x轴上的一个动点,连接CD,将△ACD绕点C逆时针旋转60°得到△BCE,连接DE.
(1)点C的坐标为____,△CDE为____三角形;
(2)当点D在线段AB上运动时,四边形CDBE的周长是否存在最小值?若存在,求出四边形CDBE的周长最小值及此时点D的坐标;若不存在,请说明理由;
(3)当△BDE是直角三角形时,请直接写出点D的坐标.
【答案】(1)(3,3![]() );等边;(2)存在,6+6
);等边;(2)存在,6+6![]() ,(3,0);(3)(-6,0)或(12,0).
,(3,0);(3)(-6,0)或(12,0).
【解析】
(1)作CH⊥AB于H,根据直角三角形的性质求出AH,根据勾股定理求出CH,得到点C的坐标,根据旋转变换的性质、等边三角形的判定定理得到△CDE为等边三角形;
(2)证明△ACD≌△BCE,得到AD=BE,根据四边形的周长公式、垂线段最短计算,求出四边形CDBE的周长最小值、此时点D的坐标;
(3)分点的D在AB的延长线、在BA的延长线两种情况,根据直角三角形的性质、等边三角形的性质解答.
解:(1)如图①,作CH⊥AB于H,

∵△ABC为等边三角形,
∴CA=CB=AB=6,
∵CH⊥AB,
∴AH=HB=3,
由勾股定理得,CH=![]() ,
,
∴点C的坐标为(3,3![]() ),
),
由旋转的性质可知,CD=CE,∠DCE=60°,
∴△CDE为等边三角形,
故答案为:(3,3![]() );等边;
);等边;
(2)存在,
理由如下:∵△ABC为等边三角形,
∴∠ACD+∠DCB=60°,
∵△DCE为等边三角形,
∴∠BCE+∠DCB=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中, ,
,
∴△ACD≌△BCE(SAS)
∴AD=BE,
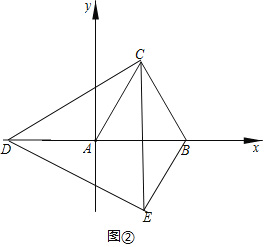
∴四边形CDBE的周长=CD+DB+BE+CE=CD+DB+AD+CE=6+2CD,
当CD最小时,四边形CDBE的周长存在最小值,
由垂线段最短可知,CD⊥AB时,CD最小,CD的最小值为3![]() ,
,
∴四边形CDBE的周长最小值为6+6![]() ,此时点D的坐标为(3,0);
,此时点D的坐标为(3,0);
(3)由(2)可知,△ACD≌△BCE,
∴BE=AD,
∴∠DBE=120°或60°,不能为90°,
如图②,∠DEB=90°时,∠DBE=60°,
∴∠BDE=30°,
∴DB=2BE,
∵BE=AD,
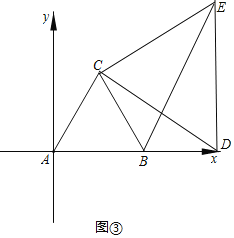
∴AD=AB=6,此时,点D的坐标为(-6,0),
如图③,当∠BDE=90°时,∠ADC=90°-60°=30°,
∵∠CAD=60°,
∴∠ACD=90°,又∠ADC=30°,
∴AD=2AC=12,此时,点D的坐标为(12,0),
综上所述,当△BDE是直角三角形时,点D的坐标为(-6,0)或(12,0).


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】小亮妈妈下岗后开了一家糕点店,现有10.2千克面粉,10.2千克鸡蛋,计划加工一般糕点和精制糕点两种产品共50盒.

⑴有哪几种符合题意的加工方案?请你帮忙设计出来;
⑵若销售一般糕点和精制糕点的利润分别为1.5元/盒和2元/盒,试问哪种方案使小亮妈妈可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:① BC平分∠ABE;② AC∥BE;③ ∠CBE+∠D=90°;④ ∠DEB=2∠ABC.其中正确结论的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨梅是漳州的特色时令水果.杨梅一上市,水果店的老板用1200元购进一批杨梅,很快售完;老板又用2500元购进第二批杨梅,所购件数是第一批的2倍,但进价每件比第一批多了5元.
(1)第一批杨梅每件进价多少元?
(2)老板以每件150元的价格销售第二批杨梅,售出![]() 后,为了尽快售完,决定打折促销.要使得第二批杨梅的销售利润不少于320元,剩余的杨梅每件售价至少打几折(利润
后,为了尽快售完,决定打折促销.要使得第二批杨梅的销售利润不少于320元,剩余的杨梅每件售价至少打几折(利润![]() 售价
售价![]() 进价)?
进价)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出定义,若一个四边形中存在相邻两边的平方和等于任意一条对角线的平方,则称该四边形为勾股四边形.
(1)请在你学过的特殊四边形中,写出两种勾股四边形______、______;
(2)如图,将钝角△ABC绕点B顺时针旋转60°得到△DBE,连接AD、DC、CE,若∠DCE=90°.求证:四边形ABCD为勾股四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.两条对角线相等且有一个角是直角的四边形是矩形
C.平行四边形两条对角线的平方和等于四条边的平方和
D.有一条对角线平分一组对角的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
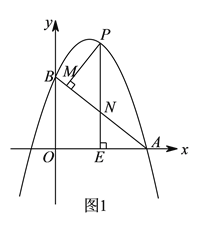
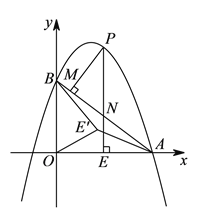
【题目】如图![]() ,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(![]() )分别求出直线AB和抛物线的函数表达式;
)分别求出直线AB和抛物线的函数表达式;
(![]() )设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
(![]() )如图2,在(
)如图2,在(![]() )条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
)条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
①在x轴上找一点Q,使△OQE'∽△OE'A,并求出Q点的坐标;
②求BE'+![]() AE'的最小值.
AE'的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
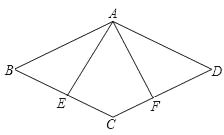
【题目】已知:如图,在菱形ABCD中,E、F分别是BC、CD的中点.
(1)求证:△ABE≌△ADF;
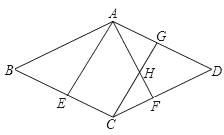
(2)过点C作CG∥EA交AF于H,交AD于G,若∠BAE=25°,∠BCD=130°,求∠AHC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com