
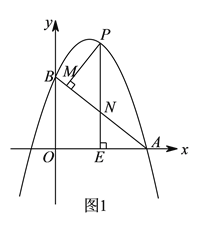
【题目】如图![]() ,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(![]() )分别求出直线AB和抛物线的函数表达式;
)分别求出直线AB和抛物线的函数表达式;
(![]() )设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
(![]() )如图2,在(
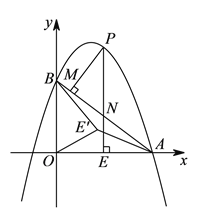
)如图2,在(![]() )条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
)条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
①在x轴上找一点Q,使△OQE'∽△OE'A,并求出Q点的坐标;
②求BE'+![]() AE'的最小值.
AE'的最小值.
【答案】(1)![]() ;
; ![]() ;(2)4;(3)①
;(2)4;(3)①![]() ,②
,②![]() .
.
【解析】分析:(1)把点A(8,0)代入抛物线y=ax-6ax+6,可求得a的值,从而可得到抛物线的解析式,然后求得点A和点B的坐标,最后利用待定系数法可求得直线AB的解析式;
(2)E(m,0),则N(m,-![]() m+6),P(m,
m+6),P(m, ![]() +6),然后证明△ANE∽△ABO,依据相似三角形的性质可求得AN的长,接下来,再证明△NMP∽△NEA,然后依据相似三角形的性质可得到
+6),然后证明△ANE∽△ABO,依据相似三角形的性质可求得AN的长,接下来,再证明△NMP∽△NEA,然后依据相似三角形的性质可得到![]() ,从而可求得PM=12-
,从而可求得PM=12-![]() m,然后依据PM=
m,然后依据PM=![]() m+3m,然后列出关于m的方程求解即可;
m+3m,然后列出关于m的方程求解即可;
(3)①在(2)的条件下,m=4,则OE′=OE=4,然后再证明△OQE′∽△OE′A,依据相似三角形的性质可得到![]() ,从而可求得OQ的值,于是可得到点Q的坐标;
,从而可求得OQ的值,于是可得到点Q的坐标;
②由①可知,当Q为(2,0)时,△OQE′∽△OE′A,且相似比为![]() ,于是得到BE′+
,于是得到BE′+![]() AE′=BE′+QE′,当点B、Q、E′在一条直线上时,BE′+QE′最小,最小值为BQ的长.
AE′=BE′+QE′,当点B、Q、E′在一条直线上时,BE′+QE′最小,最小值为BQ的长.
本题解析:
(![]() )把点
)把点![]() 代入抛物线
代入抛物线![]()
得![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() 与
与![]() 轴交点,令
轴交点,令![]() ,
,
得![]() ,
,
∴![]() .
.
设![]() 为
为![]() 过
过![]() ,
, ![]() ,
,
∴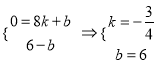 ,
,
∴![]() .
.
(![]() )∵过
)∵过![]() 作
作![]() 轴垂线交
轴垂线交![]() 于
于![]() ,交抛物线于
,交抛物线于![]() ,
,
∵![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴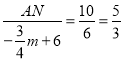 ,
,
∴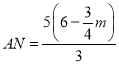 ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴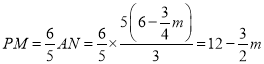 ,
,
∵![]() ,
,
∴![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() .
.
(![]() )①在(
)①在(![]() )的条件下,
)的条件下, ![]() ,∴
,∴![]() ,
,
设![]() ,∵旋转,∴
,∵旋转,∴![]() ,
,
若![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
②由①可知,当![]() 为
为![]() 时,
时,
![]() ,且相似比为
,且相似比为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() 旋转到
旋转到![]() 所在直线上时,
所在直线上时, ![]() 最小,即为
最小,即为![]() 长度,
长度,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】已知:![]() 平行线
平行线![]() 与
与![]() 与
与![]() 与
与![]() 之间的距离分别为
之间的距离分别为![]() 且
且![]()
![]() ,
,![]() .我们把四个顶点分别在
.我们把四个顶点分别在![]() 这四条平行线上的四边形称为“线上四边形”
这四条平行线上的四边形称为“线上四边形”
(1)如图1,正方形![]() 为“线上四边形”,
为“线上四边形”,![]() 于点
于点![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .求正方形
.求正方形![]() 的边长.
的边长.

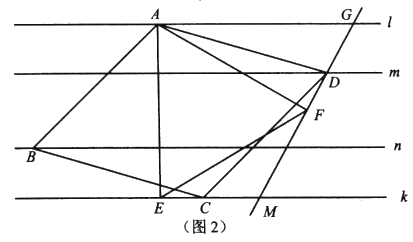
(2)如图2,菱形![]() 为“线上四边形”且
为“线上四边形”且![]() 是等边三角形,点
是等边三角形,点![]() 在直线
在直线![]() 上,连接
上,连接![]() 且
且![]() 的延长线分别交直线
的延长线分别交直线![]() 于点
于点![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2=![]() 的图象相交于A,B两点,点B的坐标为(2m,-m).
的图象相交于A,B两点,点B的坐标为(2m,-m).
(1)求出m值并确定反比例函数的表达式;
(2)请直接写出当x<m时,y2的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
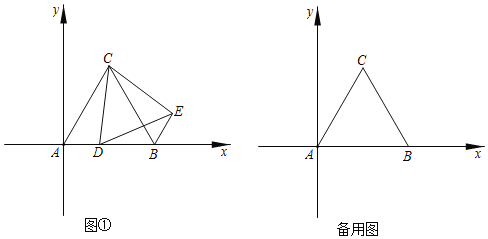
【题目】如图,在平面直角坐标系中,等边△ABC的顶点A,B的坐标分别为(0,0),(6,0),点D是x轴上的一个动点,连接CD,将△ACD绕点C逆时针旋转60°得到△BCE,连接DE.
(1)点C的坐标为____,△CDE为____三角形;
(2)当点D在线段AB上运动时,四边形CDBE的周长是否存在最小值?若存在,求出四边形CDBE的周长最小值及此时点D的坐标;若不存在,请说明理由;
(3)当△BDE是直角三角形时,请直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(4,0),B(2,0),若点C在一次函数y=![]() x+2的图象上,且△ABC为直角三角形,则满足条件的点C有( )
x+2的图象上,且△ABC为直角三角形,则满足条件的点C有( )
A.4个B.2个C.3个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商铺进行维修,若请甲、乙两名工人同时施工,![]() 天可以完成,共需支付两人工资
天可以完成,共需支付两人工资![]() 元,若先请甲工人单独做
元,若先请甲工人单独做![]() 天,再请乙工人单独做
天,再请乙工人单独做![]() 天也可完成,共需付给两人工资
天也可完成,共需付给两人工资![]() 元
元
![]() 甲、乙工人单独工作一天,商铺应分别支付多少工资?
甲、乙工人单独工作一天,商铺应分别支付多少工资?
![]() 单独请哪名工人完成,商铺支付维修费用较少?
单独请哪名工人完成,商铺支付维修费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
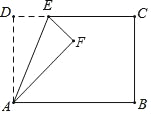
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)如图,平行四边形OBCD中,OB=8cm,BC=6cm,∠DOB=45°,点P从O沿OB边向点B移动,点Q从点B沿BC边向点C移动,P,Q同时出发,速度都是1cm/s.
(1)求经过O,B,D三点的抛物线的解析式;
(2)判断P,Q移动几秒时,△PBQ为等腰三角形;
(3)若允许P点越过B点在BC上运动,Q点越过C点在CD上运动,设线PQ与OB,BC,DC围成的图形面积为y(cm2),点P,Q的移动时间为t(s),请写出y与t之间的函数关系式,并写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.

(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com