
【题目】如图,![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.(请填空完成下面的解答,其中括号内填说理的依据)
的度数.(请填空完成下面的解答,其中括号内填说理的依据)
解:因为![]()
所以 (同旁内角互补,两直线平行)
所以![]() 又因为
又因为![]() ,所以 (等量代换)
,所以 (等量代换)
所以![]() 所以
所以![]() 又因为
又因为![]()
所以![]() .
.

【答案】答案见解析.
【解析】
根据平行线的判定得出AB∥EF,根据平行线的性质得出∠ADE=∠3,求出∠ADE=∠B,根据平行线的判定得出DE∥BC;根据平行线的性质得出∠C+∠DEC=180°,即可求出答案.
解:因为∠1+∠2=180°
所以AB∥EF(同旁内角互补,两直线平行)
所以∠ADE=∠3(两直线平行,内错角相等)
又因为∠B=∠3
所以∠ADE=∠B(等量代换)
所以DE∥BC(同位角相等,两直线平行)
所以∠C+∠DEC=180°(两直线平行,同旁内角互补)
又因为∠C=65°
所以∠DEC=180°-∠C=180°-65°=115°
故答案为:AB∥EF;两直线平行,内错角相等;∠ADE=∠B;同位角相等,两直线平行;两直线平行,同旁内角互补.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,点
,点![]() 是直线
是直线![]() 、
、![]() 之间的一点,连接
之间的一点,连接![]() 、
、![]() .
.
(1)探究猜想:
①若![]() ,则
,则![]() .
.
②若![]() ,则
,则![]() .
.
③猜想图1中![]() 、
、![]() 、
、![]() 的关系,并证明你的结论.
的关系,并证明你的结论.
(2)拓展应用:
如图2,![]() ,线段
,线段![]() 把
把![]() 这个封闭区域分为I、II两部分(不含边界),点
这个封闭区域分为I、II两部分(不含边界),点![]() 是位于这两个区域内的任意一点,请直接写出
是位于这两个区域内的任意一点,请直接写出![]() 、
、![]() 、
、![]() 的关系.
的关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD,MN分别交AB,CD于点E,F,∠BEF与∠DFE的两条平分线相交于点P1,∠BEP1与∠DFP1的两条平分线相交于点P2,则∠P2的度数为_______.
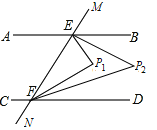
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,射线
,射线![]() 在
在![]() 内(如图1).
内(如图1).
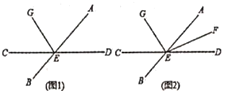
(1)若![]() 比
比![]() 小25度,求
小25度,求![]() 的大小;
的大小;
(2)若射线![]() 平分
平分![]() ,
,![]() (如图2),则
(如图2),则![]() (用含
(用含![]() 的代数式表示,请直接写出结果)
的代数式表示,请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一个由小正方体组成的几何体的左视图和俯视图.

![]() 该几何体最少需要几块小正方体?最多可以有几块小正方体?
该几何体最少需要几块小正方体?最多可以有几块小正方体?
![]() 请画出该几何体的所有可能的主视图.
请画出该几何体的所有可能的主视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB与△OCD是以点0为位似中心的位似图形,相似比为1:2,∠OCD=90![]() ,CO=CD.若B(2,0),则点C的坐标为( )
,CO=CD.若B(2,0),则点C的坐标为( )
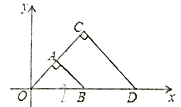
A. (2,2) B. (1,2) C. (![]() ,2
,2![]() ) D. (2,1)
) D. (2,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com