
 如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1000人,则根据此估计步行上学的有400人.
如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1000人,则根据此估计步行上学的有400人.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
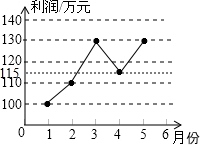 某企业1-5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( )
某企业1-5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( )| A. | 1-5月份利润的众数是130万元 | |
| B. | 1-4月份利润的极差与1-5月份利润的极差不同 | |
| C. | 1-2月份利润的增长快于2-3月份利润的增长 | |
| D. | 1-5月份利润的中位数是130万元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
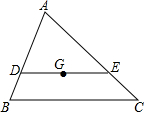 如图,G为△ABC的重心,DE过点G,且DE∥BC,交AB、AC,分别于D、E两点,则△ADE与△ABC的面积之比为$\frac{4}{9}$.
如图,G为△ABC的重心,DE过点G,且DE∥BC,交AB、AC,分别于D、E两点,则△ADE与△ABC的面积之比为$\frac{4}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
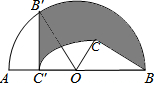 如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为πcm2.
如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为πcm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>0>y2 | B. | y2>0>y1 | C. | y1>y2>0 | D. | y2>y1>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com