
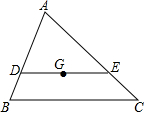
 如图,G为△ABC的重心,DE过点G,且DE∥BC,交AB、AC,分别于D、E两点,则△ADE与△ABC的面积之比为$\frac{4}{9}$.
如图,G为△ABC的重心,DE过点G,且DE∥BC,交AB、AC,分别于D、E两点,则△ADE与△ABC的面积之比为$\frac{4}{9}$. 分析 连接AG并延长交BC于H,根据重心的概念得到AG=2GH,根据平行线的性质、相似三角形的性质计算即可.
解答 解: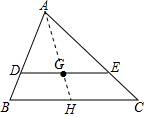 连接AG并延长交BC于H,
连接AG并延长交BC于H,
∵G为△ABC的重心,
∴AG=2GH,
∵DE∥BC,
∴$\frac{AD}{AB}$=$\frac{AG}{AH}$=$\frac{2}{3}$,
∵DE∥BC,
∴△ADE∽△ABC,相似比为$\frac{2}{3}$,
∴△ADE与△ABC的面积之比为$\frac{4}{9}$,
故答案为:$\frac{4}{9}$.
点评 本题考查的是三角形的重心的概念、相似三角形的判定和性质,三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:填空题
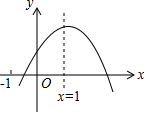 已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②a-b+c<0;③2a+b-c<0;④4a+2b+c>0,⑤若点(-$\frac{2}{3}$,y1)和($\frac{7}{3}$,y2)在该图象上,则y1>y2.其中正确的结论是②③④(填入正确结论的序号)
已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②a-b+c<0;③2a+b-c<0;④4a+2b+c>0,⑤若点(-$\frac{2}{3}$,y1)和($\frac{7}{3}$,y2)在该图象上,则y1>y2.其中正确的结论是②③④(填入正确结论的序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
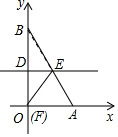 将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A($\sqrt{3}$,0),点B(0,3),点O(0,0)
将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A($\sqrt{3}$,0),点B(0,3),点O(0,0)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1000人,则根据此估计步行上学的有400人.
如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1000人,则根据此估计步行上学的有400人.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
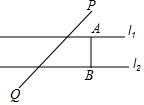 如图,已知直线l1∥l2,l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4$\sqrt{30}$,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ=16.
如图,已知直线l1∥l2,l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4$\sqrt{30}$,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ=16.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
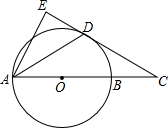 如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com