
【题目】如图1,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于G,连接DG.
(1)求∠EDG的度数.
(2)如图2,E为BC的中点,连接BF.
①求证:BF∥DE;
②若正方形边长为12,求线段AG的长.


【答案】(1)45°;(2)①用外角证明平行见解析,②4
【解析】整体分析:
(1)判断DE,DG分别平分∠CDF,∠ADF;(2)①由ED平分∠CEG,EF=EB,结合三角形的一个外角等于和它不相邻的两个内角的和得到∠CED=∠EBF;(3)由(1)中的结论,在Rt△BEG中用勾股定理列方程求解.
(1)解:由折叠知,DF=DC,∠CDE=∠FDE,∠DFE=∠DCE=90°,
∵AD=CD,所以AD=DF,
∵∠DAG=90°,DG=DG,
∴△DAG≌△DFG,∴∠ADG=∠FDG,
∴∠EDG=∠EDF+∠FDG=![]() (∠CDF+∠FDA)=
(∠CDF+∠FDA)=![]() ×90°=45°.
×90°=45°.
(2)①证明:由折叠知,CE=EF,∠CED=∠FED,
∵E为BC的中点,∴BE=CE,∴EF=BE,
∴∠EBF=∠EFB,
∵∠CEG=∠EBF+∠EFB,∴∠CED=∠EBF,
∴BF∥DE.
(3)由(1)得EC=EF,GA=GF,
∴EG=EC+GA.
设AG=x,则BG=12-x,
又EB=EC=EF=6,
在Rt△BEG中,由勾股定理得:BG2+BE2=EG2.
∴(12-x)2+62=(x+6)2,解得x=4.
所以线段AG的长为4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
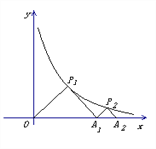
【题目】如图, △P1OA1与△P2A1A2是等腰直角三角形,点![]() 、
、![]() 在函数
在函数![]() 的图象上,斜边
的图象上,斜边![]() 、
、![]() 都在
都在![]() 轴上,则点
轴上,则点![]() 的坐标是____________.
的坐标是____________.
【答案】(![]() ,0)
,0)
【解析】因为△P1OA1是等腰直角三角形,所以设P1(a,a),则a2=4,a=2,所以OA1=2×2=4,又因为△P2A1A2是等腰直角三角形,设P2(4+b,b),所以b(4+b)=4,解得b=![]() ,所以A1A2=
,所以A1A2=![]() ,所以OA2=
,所以OA2=![]() +4=
+4=![]() ,则A2(
,则A2(![]() ,0),故答案为(
,0),故答案为(![]() ,0).
,0).
【题型】填空题
【结束】
16
【题目】如图,函数y=![]() 和y=
和y=![]() 在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________
在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们的生活水平的提高,家用轿车越来越多地进入家庭.小明家买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣9 | ﹣13 | 0 | ﹣14 | ﹣16 | +33 | +19 |
(1)求出这7天的行驶路程中最多的一天比最少的一天多行驶多少千米?
(2)若每行驶100km需用汽油8升,每升汽油6.5元,计算小明家这7天的汽油费用共是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】售货员:“快来买啦,特价鸡蛋,原价每箱14元,现价每箱12元,每箱有鸡蛋30个.”
顾客甲:“我店里买了一些这种特价鸡蛋,花的钱比按原价买同样多鸡蛋花的钱的2倍少96元.”
乙顾客:“我家买了两箱相同特价的鸡蛋,结果18天后,剩下的20个鸡蛋全坏了.”
请你根据上面的对话,解答下面的问题:
(1)顾客乙买的两箱鸡蛋合算吗?说明理由.
(2)请你求出顾客甲店里买了多少箱这种特价鸡蛋,假设这批特价鸡蛋的保质期还有18天,那么甲店里平均每天要消费多少个鸡蛋才不会浪费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】情景观察:如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 ,并写出证明过程.
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com