Question

【题目】情景观察：如图1，△ABC中，AB=AC，∠BAC=45°，CD⊥AB，AE⊥BC，垂足分别为D、E，CD与AE交于点F．

①写出图1中所有的全等三角形　 　；

②线段AF与线段CE的数量关系是　 　，并写出证明过程．

问题探究：

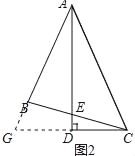
如图2，△ABC中，∠BAC=45°，AB=BC，AD平分∠BAC，AD⊥CD，垂足为D，AD与BC交于点E．

求证：AE=2CD．

Answer 1

【答案】①△ABE≌△ACE，△ADF≌△CDB；②AF=2CE，详见解析.

【解析】试题分析：

情景观察：①由AB＝AC，AE⊥BC，AE是公共边，根据“HL”即可判断△ABE≌△ACE；根据等腰三角形“三线合一”和∠A＝45°，可求得∠DAF＝22.5°，利用等边对等角和三角形内角和定理求得∠B＝67.5°，在Rt△BDC中即可求得∠DCB＝22.5°，在Rt△ADC中由∠A＝45°可得AD＝CD，由“ASA”即可得出△ADF≌△CDB；

②由①中△ADF≌△CDB得出AF＝BC，再由“三线合一”得出BC＝2CE，等量代换即可得出结论；

问题探究：延长AB、CD交于点G，由ASA证明△ADC≌△ADG，得出对应边相等CD＝GD，即CG＝2CD，证出∠BAE＝∠BCG，由ASA证明△ABE≌△CBG，得出AE＝CG＝2CD即可．

试题解析：

解：①图1中所有的全等三角形为△ABE≌△ACE，△ADF≌△CDB；

故答案为：△ABE≌△ACE，△ADF≌△CDB；

②线段AF与线段CE的数量关系是：AF＝2CE；

故答案为：AF＝2CE．

证明：∵△BCD≌△FAD，

∴AF＝BC，

∵AB＝AC，AE⊥BC，

∴BC＝2CE，

∴AF＝2CE；

问题探究：

证明：延长AB、CD交于点G，如图2所示：

∵AD平分∠BAC，

∴∠CAD＝∠GAD，

∵AD⊥CD，

∴∠ADC＝∠ADG＝90°，

在△ADC和△ADG中，

，

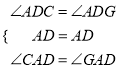∴△ADC≌△ADG（ASA），

∴CD＝GD，即CG＝2CD，

∵∠BAC＝45°，AB＝BC，

∴∠ABC＝90°，

∴∠CBG＝90°，

∴∠G＋∠BCG＝90°，

∵∠G＋∠BAE＝90°，

∴∠BAE＝∠BCG，

在△ABE和△CBG中，

，

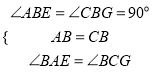∴△ABE≌△CBG（ASA），

∴AE＝CG＝2CD．