
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3 , …组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2015秒时,点P的坐标是( )
个单位长度,则第2015秒时,点P的坐标是( )
A.(2014,0)
B.(2015,﹣1)
C.(2015,1)
D.(2016,0)
【答案】B
【解析】解:半径为1个单位长度的半圆的周长为: 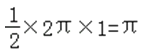 ,
,
∵点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,
个单位长度,
∴点P1秒走![]() 个半圆,
个半圆,
当点P从原点O出发,沿这条曲线向右运动,运动时间为1秒时,点P的坐标为(1,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为2秒时,点P的坐标为(2,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为3秒时,点P的坐标为(3,﹣1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为4秒时,点P的坐标为(4,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为5秒时,点P的坐标为(5,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为6秒时,点P的坐标为(6,0),
…,
∵2015÷4=503…3
∴A2015的坐标是(2015,﹣1),
故选:B.
根据图象可得移动4次图象完成一个循环,从而可得出点A2015的坐标.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以O为圆心的弧BD度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
(1)求![]() 的值;
的值;
(2)若OE与弧BD交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;(3)在(2)的条件下,若BC=1,求tan∠BCO的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东门天虹商场购进一批“童乐”牌玩具,每件成本价30元,每件玩具销售单价x(元)与每天的销售量y(件)的关系如下表:
x(元) | … | 35 | 40 | 45 | 50 | … |
y(件) | … | 750 | 700 | 650 | 600 | … |
若每天的销售量y(件)是销售单价x(元)的一次函数
(1)求y与x的函数关系式;
(2)设东门天虹商场销售“童乐”牌儿童玩具每天获得的利润为w(元),当销售单价x为何值时,每天可获得最大利润?此时最大利润是多少?
(3)若东门天虹商场销售“童乐”牌玩具每天获得的利润最多不超过15000元,最低不低于12000元,那么商场该如何确定“童乐”牌玩具的销售单价的波动范围?请你直接给出销售单价x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A,B在数轴上对应的数分别用a,b表示,且(![]() ab+100)2+|a﹣20|=0,P是数轴上的一个动点.
ab+100)2+|a﹣20|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离.
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数.
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度第四次向右移动7个单位长度,….点P能移动到与A或B重合的位置吗?若都不能,请直接回答.若能,请直接指出,第几次移动与哪一点重合?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣1.
(1)求此二次函数的图象与x轴的交点坐标;
(2)将y=x2的图象经过怎样的平移,就可以得到二次函数y=x2﹣2x﹣1的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读题画图计算并作答
画线段AB=3 cm,在线段AB上取一点K,使AK=BK,在线段AB的延长线上取一点C,使AC=3BC,在线段BA的延长线取一点D,使AD=![]() AB.
AB.
(1)求线段BC、DC的长?
(2)点K是哪些线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,地震、泥石流等自然灾害频繁发生,造成极大的生命和财产损失.为了更好地做好“防震减灾”工作,我市相关部门对某中学学生“防震减灾”的知晓率采取随机抽样的方法进行问卷调查,调查结果分为“非常了解”、“比较了解”、“基本了解”和“不了解”四个等级.小明根据调查结果绘制了如下统计图,请根据提供的信息回答问题: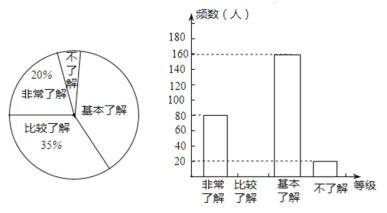
(1)本次参与问卷调查的学生有多少人;扇形统计图中“基本了解”部分所对应的扇形圆心角是多少度;在该校2000名学生中随机提问一名学生,对“防震减灾”不了解的概率为多少.
(2)请补全频数分布直方图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com