
【题目】(探究过程题)用直接开平方法解一元二次方程4(2x﹣1)2﹣25(x+1)2=0.
解:移项得4(2x﹣1)2=25(x+1)2,①
直接开平方得2(2x﹣1)=5(x+1),②
∴x=﹣7. ③
上述解题过程,有无错误如有,错在第_____步,原因是_____,请写出正确的解答过程_____.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP(备注:当EF=FP,∠EFP=90°时,∠PEF=∠FPE=45°,反之当∠PEF=∠FPE=45°时,当EF=FP).
(1)在图1中,请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系.
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的结论还成立吗?若成立,给出证明:若不成立,请说明理由.
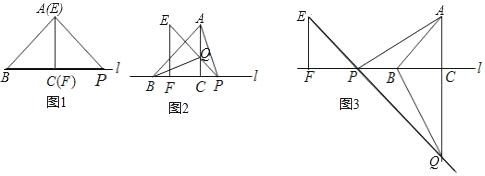
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省道S226在我县境内某路段实行限速,机动车辆行驶速度不得超过60km/h,如图,一辆小汽车在这段路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方36m的C处,过了3s后,测得小汽车与车速检测仪间距离为60m,这辆小汽车超速了吗?
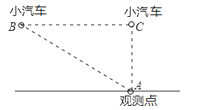
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天) | 豪华间(元/人/天) | 贵宾间(元/人/天) | |
三人间 | 50 | 100 | 500 |
双人间 | 70 | 150 | 800 |
单人间 | 100 | 200 | 1500 |
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数;
(1)若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大;几个月后,能收回投资?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=x2+mx+n的图象经过A(0,3),且对称轴是直线x=2.
(1)求该函数的解析式;
(2)在抛物线上找一点P,使△PBC的面积是△ABC的面积的![]() ,求出点P的坐标.
,求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个水槽有进水管和出水管各一个,进水管每分钟进水a升,出水管每分钟出水b升.水槽在开始5分钟内只进水不出水,随后15分钟内既进水又出水,得到时间x(分)与水槽内的水量y(升)之间的函数关系(如图所示).
(1)求a、b的值;
(2)如果在20分钟之后只出水不进水,求这段时间内y关于x的函数解析式及定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意结合图形填空:
已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.

答:是,理由如下:
∵AD⊥BC,EG⊥BC(___________)
∴∠4=∠5=90°(___________________________)
∴AD∥EG(________________________________)
∴∠1=∠E____________________________)
∠2=∠3(__________________________________)
∵∠E=∠3(________________)
∴________________( 等量代换 )
∴AD是∠BAC的平分线(_____________________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com