
 轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线
轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线 与扇形OAB的边界总有两个公共点,则实数
与扇形OAB的边界总有两个公共点,则实数 的取值范围是 .
的取值范围是 .
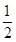 .
.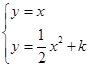
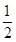 时,抛物线与OA有一个交点,
时,抛物线与OA有一个交点,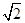 ,
,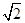 ),
),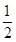 ×4+k=0,
×4+k=0,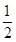 x2+k与扇形OAB的边界总有两个公共点,实数k的取值范围是-2<k<
x2+k与扇形OAB的边界总有两个公共点,实数k的取值范围是-2<k<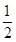 .
.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源:不详 题型:解答题
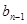 ,0)和An(bn,0).当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
,0)和An(bn,0).当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.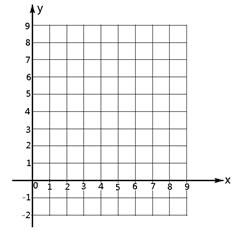
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 x2交于A、B两点.
x2交于A、B两点.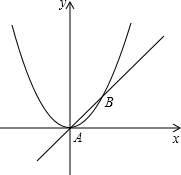
 x2的函数值为y2.若y1>y2,求x的取值范围.
x2的函数值为y2.若y1>y2,求x的取值范围.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
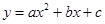 (a≠0)的图象,则下列说法:①a>0 ②2a+b="0" ③a+b+c>0 ④当﹣1<x<3时,y>0其中正确的个数为( ).
(a≠0)的图象,则下列说法:①a>0 ②2a+b="0" ③a+b+c>0 ④当﹣1<x<3时,y>0其中正确的个数为( ).
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com