
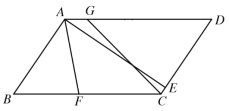
【题目】如图,在平行四边形![]() 中,过
中,过![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)过H作HP⊥AD交AD于点P,在Rt△PGH中求出PH,在Rt△APH中利用正切求出AP,再利用勾股定理求AH,即可得AF的长;
(2)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点K,交AE于点
于点K,交AE于点![]() ,易得四边形AFKG为平行四边形,得到
,易得四边形AFKG为平行四边形,得到![]() ,然后证明∠AMH=45°=∠GCK,
,然后证明∠AMH=45°=∠GCK,![]() ,可证
,可证![]() ≌
≌![]() ,得GC=AM,利用等量代换即可求证结论.
,得GC=AM,利用等量代换即可求证结论.
(1)如图,过H作HP⊥AD交AD于点P,
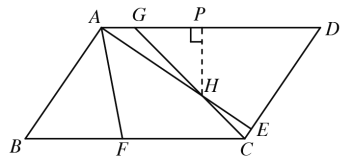
∵在平行四边形![]() 中,AD∥BC,∠GCF=45°
中,AD∥BC,∠GCF=45°
∴∠PGH=45°
在Rt△PGH中,GH=4,
∴PH=![]()
在Rt△APH中,![]()
∴![]()
![]()
又∵![]()
∴![]()
(2)如图,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点K,交AE于点
于点K,交AE于点![]() .
.
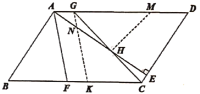
∵AG∥FK,AF∥GK
∴四边形AFKG为平行四边形
∴![]()
由(1)可知∠HGM=45°,
∵HM⊥GH,
∴∠AMH=45°=∠GCK
又∵AF∥GK
∴![]()
∵![]() ,
,![]()
∴![]()
在△GKC和△AHM中,
∵∠GCK=∠AMH,∠CGK=∠MAH,GK=AH,
∴![]() ≌
≌![]() (AAS)
(AAS)
∴GC=AM
又∵在等腰Rt△GHM中,GM=![]() GH
GH
∴AM=AG+GM=AG+![]() GH
GH
∴![]()


科目:初中数学 来源: 题型:
【题目】小红将笔记本电脑水平放置在桌子上,当显示屏![]() 与底板
与底板![]() 所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图如图2. 使用时为了散热,她在底板下垫入散热架
所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图如图2. 使用时为了散热,她在底板下垫入散热架![]() 后,电脑转到
后,电脑转到![]() 位置(如图3),侧面示意图为图4. 已知
位置(如图3),侧面示意图为图4. 已知![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
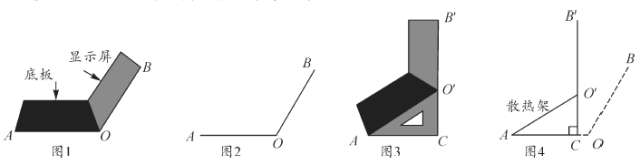
(1)求![]() 的度数.
的度数.
(2)显示屏的顶部![]() 比原来的顶部
比原来的顶部![]() 升高了多少?
升高了多少?
(3)如图4,垫入散热架后,要使显示屏![]() 与水平线的夹角仍保持120°,则显示屏
与水平线的夹角仍保持120°,则显示屏![]() 应绕点
应绕点![]() '按顺时针方向旋转多少度?并说明理由.
'按顺时针方向旋转多少度?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.
(1)试判断BC与⊙O的位置关系,并说明理由;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“康河泛舟,问道剑桥”,甲乙两人相约泛舟康河,路线均为从![]() 到
到![]() 再返回
再返回![]() ,且
,且![]() 全长2千米,甲出发2分钟后,乙以另一速度出发,结果同时到达目的
全长2千米,甲出发2分钟后,乙以另一速度出发,结果同时到达目的![]() 地,甲到达目的地拍照5分钟便原速返回
地,甲到达目的地拍照5分钟便原速返回![]() 地;乙到达
地;乙到达![]() 地后休息了2分钟,然后立即提速为原速的
地后休息了2分钟,然后立即提速为原速的![]() 倍返回
倍返回![]() 地.甲乙之间的距离
地.甲乙之间的距离![]() (单位:米)与甲的行驶时间
(单位:米)与甲的行驶时间![]() (单位:分钟)之间的函数关系如图所示.则当乙回到
(单位:分钟)之间的函数关系如图所示.则当乙回到![]() 地时,甲距离
地时,甲距离![]() 地________米.
地________米.
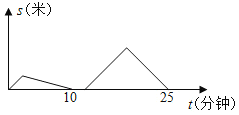
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:(1)ac<0;
(2)抛物线顶点坐标为(1,5);
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的序号为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)求点B的坐标(用含![]() 的式子表示);
的式子表示);
(2)求抛物线的对称轴;
(3)已知点![]() ,
,![]() .若抛物线与线段PQ恰有一个公共点,结合函数图象,求
.若抛物线与线段PQ恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“三农”问题的解决,某农民近两年的年收入发生了明显变化,已知前年和去年的收入分别是60000元和80000元,下面是依据①②③三种农作物每种作物每年的收入占该年年收入的比例绘制的扇形统计图.依据统计图得出的以下四个结论正确的是( )

A. ①的收入去年和前年相同
B. ③的收入所占比例前年的比去年的大
C. 去年②的收入为2.8万
D. 前年年收入不止①②③三种农作物的收入
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com