
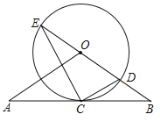
【题目】已知:如图,在△OAB中,OA=OB,⊙O经过AB的中点C,与OB交于点D,且与BO的延长线交于点E,连接EC,CD.
(1)试判断AB与⊙O的位置关系,并加以证明;
(2)若tanE=![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
【答案】(1)AB与⊙O的位置关系是相切,证明见解析;(2)OA=5.
【解析】
(1)先判断AB与⊙O的位置关系,然后根据等腰三角形的性质即可解答本题;
(2)根据题三角形的相似可以求得BD的长,从而可以得到OA的长.
解:(1)AB与⊙O的位置关系是相切,
证明:如图,连接OC.
∵OA=OB,C为AB的中点,
∴OC⊥AB.
∴AB是⊙O的切线;
(2)∵ED是直径,
∴∠ECD=90°.
∴∠E+∠ODC=90°.
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,
∴∠BCD=∠E.
又∵∠CBD=∠EBC,
∴△BCD∽△BEC.
∴![]() .
.
∴BC2=BDBE.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
设BD=x,则BC=2x.
又BC2=BDBE,
∴(2x)2=x(x+6).
解得x1=0,x2=2.
∵BD=x>0,
∴BD=2.
∴OA=OB=BD+OD=2+3=5.


科目:初中数学 来源: 题型:
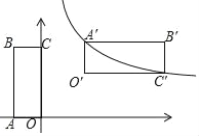
【题目】如图,在平面直角坐标系中,矩形OABC的边OA与x轴重合,B的坐标为(﹣1,2),将矩形OABC绕平面内一点P顺时针旋转90°,使A、C两点恰好落在反比例函数![]() 的图象上,则旋转中心P点的坐标是( )
的图象上,则旋转中心P点的坐标是( )
A. (![]() ,﹣
,﹣![]() ) B. (
) B. (![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,﹣
,﹣![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
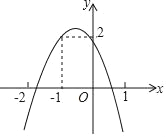
【题目】如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1、x2,其中﹣2<x1<﹣1,0<x2<1.下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③abc<0;④b2+8a<4ac.
其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC和CD于点P,Q.
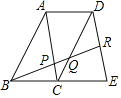
(1)求证:△ABP∽△DQR;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计划建一个长方形养鸡场,为了节省材料,利用一道足够长的墙做为养鸡场的一边,另三边用铁丝网围成,如果铁丝网的长为35m.
(1)计划建养鸡场面积为150m2,则养鸡场的长和宽各为多少?
(2)能否建成的养鸡场面积为160m2?如果能,请算出养鸡场的长和宽;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程x2-2(m+1)x+m2=0.
(1)当m取何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求这两个根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com