
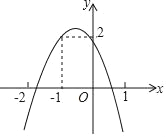
【题目】如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1、x2,其中﹣2<x1<﹣1,0<x2<1.下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③abc<0;④b2+8a<4ac.
其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
首先根据抛物线的开口方向可得到a<0,抛物线交y轴于正半轴,则c>0,而抛物线与x轴的交点中,﹣2<x1<﹣1、0<x2<1说明抛物线的对称轴在﹣1~0之间,即x=﹣![]() >﹣1,可根据这些条件以及函数图象上一些特殊点的坐标来进行判断
>﹣1,可根据这些条件以及函数图象上一些特殊点的坐标来进行判断
由图知:抛物线的开口向下,则a<0;抛物线的对称轴x=﹣![]() >﹣1,且c>0;
>﹣1,且c>0;
①由图可得:当x=﹣2时,y<0,即4a﹣2b+c<0,故①正确;
②已知x=﹣![]() >﹣1,且a<0,所以2a﹣b<0,故②正确;
>﹣1,且a<0,所以2a﹣b<0,故②正确;
③抛物线对称轴位于y轴的左侧,则a、b同号,又c>0,故abc>0,所以③不正确;
④由于抛物线的对称轴大于﹣1,所以抛物线的顶点纵坐标应该大于2,即:![]() >2,由于a<0,所以4ac﹣b2<8a,即b2+8a>4ac,故④正确;
>2,由于a<0,所以4ac﹣b2<8a,即b2+8a>4ac,故④正确;
因此正确的结论是①②④.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 与
与![]() 是两个全等的等边三角形,
是两个全等的等边三角形,![]() .有下列四个结论:①
.有下列四个结论:①![]() ;②
;②![]() ;③直线
;③直线![]() 垂直平分线段
垂直平分线段![]() ;④四边形
;④四边形![]() 是轴对称图形.其中正确的结论有_____.(把正确结论的序号填在横线上)
是轴对称图形.其中正确的结论有_____.(把正确结论的序号填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
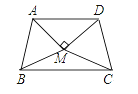
【题目】如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=26°,则∠OBC的度数为( )

A. 54°B. 64°C. 74°D. 26°
查看答案和解析>>
科目:初中数学 来源: 题型:
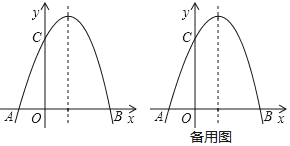
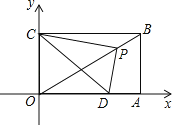
【题目】矩形OABC在平面直角坐标系中的位置如图所示,已知![]() ,点A在x轴上,点C在y轴上,P是对角线OB上一动点(不与原点重合),连接PC,过点P作
,点A在x轴上,点C在y轴上,P是对角线OB上一动点(不与原点重合),连接PC,过点P作![]() ,交x轴于点D.下列结论:①
,交x轴于点D.下列结论:①![]() ;②当点D运动到OA的中点处时,
;②当点D运动到OA的中点处时,![]() ;③在运动过程中,
;③在运动过程中,![]() 是一个定值;④当△ODP为等腰三角形时,点D的坐标为
是一个定值;④当△ODP为等腰三角形时,点D的坐标为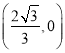 .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
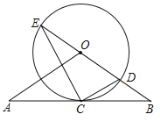
【题目】已知:如图,在△OAB中,OA=OB,⊙O经过AB的中点C,与OB交于点D,且与BO的延长线交于点E,连接EC,CD.
(1)试判断AB与⊙O的位置关系,并加以证明;
(2)若tanE=![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班数学老师将本班某次参加的数学竞赛成绩(得分取整数,满分100分)进行整理统计后,制成如下的频数直方图和扇形统计图,请根据统计图提供的信息,解答下列问题:
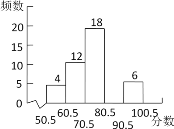
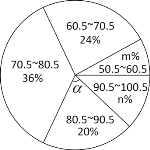
(1)在分数段70.5~80.5分的频数、频率分别是多少?
(2)m、n、![]() 的值分别是多少?
的值分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com