
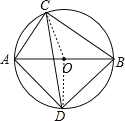
【题目】如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.

(1)求弧BC的长;
(2)求弦BD的长.
【答案】(1)![]() .(2)5
.(2)5![]() .
.
【解析】
试题分析:(1)首先根据AB是⊙O的直径,可得∠ACB=∠ADB=90°,然后在Rt△ABC中,求出∠BAC的度数,即可求出∠BOC的度数;最后根据弧长公式,求出![]() 的长即可.
的长即可.
(2)首先根据CD平分∠ACB,可得∠ACD=∠BCD;然后根据圆周角定理,可得∠AOD=∠BOD,所以AD=BD,∠ABD=∠BAD=45°;最后在Rt△ABD中,求出弦BD的长是多少即可.
试题解析:(1)如图,连接OC,OD,
 ,
,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,
∵cos∠BAC=![]() ,
,
∴∠BAC=60°,
∴∠BOC=2∠BAC=2×60°=120°,
∴![]() 的长=
的长=![]() .
.
(2)∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠AOD=∠BOD,
∴AD=BD,
∴∠ABD=∠BAD=45°,
在Rt△ABD中,
BD=AB×sin45°=10×![]() =5
=5![]() .
.


科目:初中数学 来源: 题型:
【题目】【问题情境】一节数学课后,老师布置了一道课后练习题:
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.
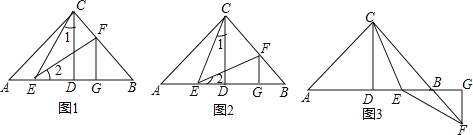
(1)阅读理解,完成解答
本题证明的思路可用下列框图表示:
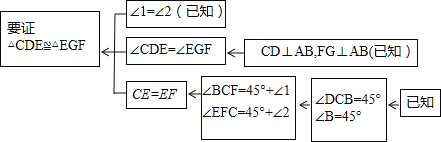
根据上述思路,请你完整地书写这道练习题的证明过程;
(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学规定:学生的学期体育综合成绩满分为100分,其中,期中考试成绩占40%,期末考试成绩占60%.小海这个学期的期中、期末体育成绩(百分制)分别是80分、90分,则小海这个学期的体育综合成绩是________分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年上半年,天津市生产总值8500.91亿元,按可比价格计算,同步增长9.2%,将“8500.91”用科学记数法可表示为( )
A. 8.50091×103 B. 8.50091×1011 C. 8.50091×105 D. 8.50091×1013
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,设A、P两点间的距离为x.
探究:
(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察到的结论;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系式,并写出x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应x的值;如果不可能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在函数y=![]() (k<0)的图象上有A(1,y1)、B(﹣1,y2)、C(﹣2,y3)三个点,则下列各式中正确的是( )
(k<0)的图象上有A(1,y1)、B(﹣1,y2)、C(﹣2,y3)三个点,则下列各式中正确的是( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y3<y1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com