
【题目】【问题情境】一节数学课后,老师布置了一道课后练习题:
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.
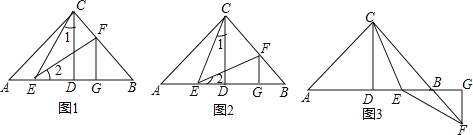
(1)阅读理解,完成解答
本题证明的思路可用下列框图表示:
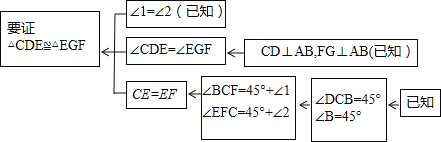
根据上述思路,请你完整地书写这道练习题的证明过程;
(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
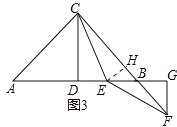
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、AE=![]() BF.
BF.
【解析】
试题分析:(1)、先证明CE=EF,根据AAS即可证明△CDE≌△EGF;(2)、先证∠ACE=∠2,再证明△ACE≌△BEF,即可得出AE=BF;(3)、作EH⊥BC与H,设DE=x,求出AE=3x,再证出BF=![]() x,即可得出结论.
x,即可得出结论.
试题解析:(1)、∵AC=BC,∠ACB=90°, ∴∠A=∠B=45°, ∵CD⊥AB, ∴∠CDB=90°,
∴∠DCB=45°, ∵∠ECF=∠DCB+∠1=45°+∠1,∠EFC=∠B+∠2=45°+∠2,∠1=∠2, ∴∠ECF=∠EFC,
∴CE=EF, ∵CD⊥AB,FG⊥AB, ∴∠CDE=∠EGF=90°,
在△CDE和△EGF中,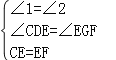 ,∴△CDE≌△EGF(AAS);
,∴△CDE≌△EGF(AAS);
(2)、由(1)得:CE=EF,∠A=∠B, ∵CE平分∠ACD, ∴∠ACE=∠1, ∵∠1=∠2,∴∠ACE=∠2,
在△ACE和△BEF中,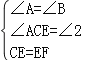 ,∴△ACE≌△BEF(AAS),∴AE=BF;
,∴△ACE≌△BEF(AAS),∴AE=BF;
(3)、AE=![]() BF,作EH⊥BC与H,如图3所示:
BF,作EH⊥BC与H,如图3所示:
设DE=x,根据题意得:BE=DE=x,AD=BD=2x,CD=AD=2x,AE=3x, 根据勾股定理得:BC=AC=2![]() x,
x,
∵∠ABC=45°,EH⊥BC, ∴BH=![]() x, ∴CH=BC﹣BH=
x, ∴CH=BC﹣BH=![]() x, ∵EC=EF, ∴FH=CH=
x, ∵EC=EF, ∴FH=CH=![]() x,
x,
∴BF=![]() x﹣
x﹣![]() x=
x=![]() x, ∴
x, ∴![]() , ∴AE=
, ∴AE=![]() BF.
BF.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点弹出一条墨线,这是因为( )
A.两点之间,线段最短
B.两点确定一条直线
C.两点之间线段的长度,叫做这两点之间的距离
D.圆上任意两点间的部分叫做圆弧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设图中每个小正方形的边长为1,
(1)请画出△ABC关于y轴对称图形△A’B’C’,其中ABC的对称点分别为A’B’C’)
(2)直接写出A’B’C’的坐标:A’B’C’
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.
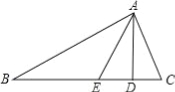
(1)求∠CAD、∠AEC和∠EAD的度数.
(2)若图形发生了变化,已知的两个角度数改为:当∠B=30°,∠C=60°则∠EAD= °;
当∠B=50°,∠C=60°时,则∠EAD= °;
当∠B=60°,∠C=60°时,则∠EAD= °;
当∠B=70°,∠C=60°时,则∠EAD= °.
(3)若∠B和∠C的度数改为用字母α和β来表示,你能找到∠EAD与α和β之间的关系吗?请直接写出你发现的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com