
����Ŀ����ͼ���ڡ�ABC�У�AD�Ǹߣ�AE�ǽ�ƽ���ߣ���B=20�㣬��C=60�㣮
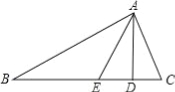
��1�����CAD����AEC�͡�EAD�Ķ�����
��2����ͼ�η����˱仯����֪�������Ƕ�����Ϊ������B=30�㣬��C=60�����EAD= �㣻
����B=50�㣬��C=60��ʱ�����EAD= �㣻
����B=60�㣬��C=60��ʱ�����EAD= �㣻
����B=70�㣬��C=60��ʱ�����EAD= �㣮
��3������B�͡�C�Ķ�����Ϊ����ĸ���ͦ�����ʾ�������ҵ���EAD����ͦ�֮��Ĺ�ϵ����ֱ��д���㷢�ֵĽ��ۣ�
���𰸡���1������CAD=30������AEC=70������EAD=20������2����15����5����0����5������3������������ʱ����EAD=���©�����������������ʱ����EAD=�������£���
��������
�����������1����������B����C�Ķ����ó���BAC�Ķ��������ݽ�ƽ���ߵ����ʵó���EAC�Ķ��������ݸ��ߵ����ʵó���CAD�Ķ�����������EAD=��EAC����DAC����AEC=180�㩁��EAC����C�ó��Ƕȣ���2����������EAD=��EAC����DAC������EAD=��DAC����EAC����Ƕȣ���3������������ʱ��������EAD=��EAC����DAC�ó��Ƕȣ���������ʱ��������EAD=��DAC����EAC�ó��Ƕ�.
�����������1�����ߡ�B=20�㣬��C=60�㣬
���BAC=180�㩁20�㩁60��=100�㣬��AE�ǽ�ƽ���ߣ����EAC=50�㣬
��AD�Ǹߣ����ADC=90�㣬���CAD=30�㣬
���EAD=��EAC����DAC=50�㩁30��=20�㣬
���AEC=180�㩁��EAC����C=180�㩁50�㩁60��=70�㣻
��2�����١�EAD=��EAC����DAC=45�㩁30��=15�㣻
�ڡ�EAD=��EAC����DAC=35�㩁30��=5�㣻
�ۡ�EAD=��EAC����DAC=30�㩁30��=0�㣻
�ܡ�EAD=��DAC����EAC=30�㩁25��=5�㣻
��3����������ʱ��
���EAD=��EAC����DAC=[��90��![]() ���㩁��90�㩁�¡㣩]=���©�������
���㩁��90�㩁�¡㣩]=���©�������
��������ʱ��
���EAD=��DAC����EAC=[��90�㩁�¡㣩����90��![]() ����]=�������£���
����]=�������£���


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м������У�����ͼ������ͼ������ͼ��ȫ��ͬ���ǣ� ��
A.Բ��
B.Բ
C.��
D.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������龳��һ����ѧ�κ���ʦ������һ���κ���ϰ�⣺
��ͼ����֪��Rt��ABC�У�AC=BC����ACB=90����CD��AB�ڵ�D����E��F�ֱ���A��BC�ϣ���1=��2��FG��AB�ڵ�G����֤����CDE�ա�EGF��
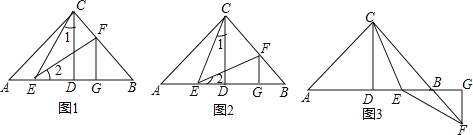
��1���Ķ����⣬��ɽ��
����֤����˼·�������п�ͼ��ʾ��
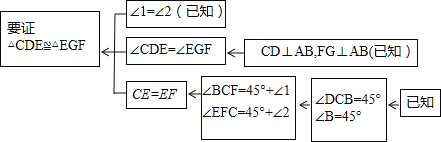
��������˼·��������������д�����ϰ���֤�����̣�
��2������λ�ã�֤������
��CEƽ����ACD�������������䣬��֤��AE=BF��
��3��֪ʶǨ�ƣ�̽������
��ͼ����֪��Rt��ABC�У�AC=BC����ACB=90����CD��AB�ڵ�D������E��DB���е㣬��F��ֱ��CB��������EC=EF����ֱ��д��AE��BF��������ϵ��������д�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�㳡��һ��ˮ�أ�ˮ�ӵ����������ͼ����ˮƽ����Ϊx�ᣬ��ˮ��Ϊԭ�㣬����ƽ��ֱ������ϵ��ˮ�ڿ��л�����������������y=��x2+4x����λ���ף���һ���֣���ˮ��������߶��ǣ� ��

A��4�� B��3�� C��2�� D��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������2��0��-1��4��6�в���һ������x��ʹ�������ݵ���λ��Ϊ3����x��ֵ��____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��һԪ���η���kx2+4x��2=0����������ȵ�ʵ��������k��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com