
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬Οφ≤ΡΝœΘΚ
–ΓΧλ‘Ύ―ßœΑ»ώΫ«»ΐΫ«Κ· ΐ÷–”ωΒΫ’β―υ“ΜΗωΈ ΧβΘΚ‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§‘ρ
Θ§‘ρ![]() ______
______
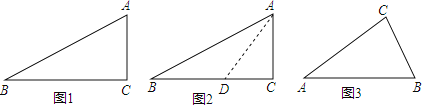
–ΓΧλΗυΨί―ßœΑΦΗΚΈΒΡΨ≠―ιΘ§œ»Μ≠≥ωΝΥΦΗΚΈΆΦ–Έ![]() »γΆΦ
»γΆΦ![]() Θ§ΥϊΖΔœ÷
Θ§ΥϊΖΔœ÷![]() ≤Μ «ΧΊ βΫ«Θ§ΒΪΥϋ «ΧΊ βΫ«
≤Μ «ΧΊ βΫ«Θ§ΒΪΥϋ «ΧΊ βΫ«![]() ΒΡ“ΜΑκΘ§»τΙΙ‘λ”–ΧΊ βΫ«ΒΡ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρΩ…ΡήΫβΨω’βΗωΈ Χβ
ΒΡ“ΜΑκΘ§»τΙΙ‘λ”–ΧΊ βΫ«ΒΡ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρΩ…ΡήΫβΨω’βΗωΈ Χβ![]() ”Ύ «–ΓΧλ≥Δ ‘Ή≈‘ΎCB±Ώ…œΫΊ»Γ
”Ύ «–ΓΧλ≥Δ ‘Ή≈‘ΎCB±Ώ…œΫΊ»Γ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() »γΆΦ
»γΆΦ![]() Θ§Ά®ΙΐΙΙ‘λ”–ΧΊ βΫ«
Θ§Ά®ΙΐΙΙ‘λ”–ΧΊ βΫ«![]() ΒΡ÷±Ϋ«»ΐΫ«–ΈΘ§Ψ≠ΙΐΆΤάμΚΆΦΤΥψ ΙΈ ΧβΒΟΒΫΫβΨωΘ°
ΒΡ÷±Ϋ«»ΐΫ«–ΈΘ§Ψ≠ΙΐΆΤάμΚΆΦΤΥψ ΙΈ ΧβΒΟΒΫΫβΨωΘ°
«κΜΊ¥πΘΚ![]() ______Θ°
______Θ°
≤ΈΩΦ–ΓΧλΥΦΩΦΈ ΧβΒΡΖΫΖ®Θ§ΫβΨωΈ ΧβΘΚ
»γΆΦ3Θ§‘ΎΒ»―ϋ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§«κΫη÷ζ
Θ§«κΫη÷ζ![]() Θ§ΙΙ‘λ≥ω
Θ§ΙΙ‘λ≥ω![]() ΒΡΫ«Θ§≤Δ«σ≥ωΗΟΫ«ΒΡ’ΐ«–÷ΒΘ°
ΒΡΫ«Θ§≤Δ«σ≥ωΗΟΫ«ΒΡ’ΐ«–÷ΒΘ°
ΓΨ¥πΑΗΓΩ![]() ,2-
,2-![]() .
.
ΓΨΫβΈωΓΩ
»γΆΦ2Θ§…η![]() Θ§
Θ§![]() ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ
ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ![]() Θ§“ΉΒΟ
Θ§“ΉΒΟ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§‘Ό‘Ύ
Θ§‘Ό‘Ύ![]() ÷–Θ§άϊ”Ο’ΐ«–Ε®“εΩ…ΦΤΥψ≥ω
÷–Θ§άϊ”Ο’ΐ«–Ε®“εΩ…ΦΤΥψ≥ω![]() Θ§Φ¥
Θ§Φ¥![]() ΘΜ
ΘΜ
»γΆΦ3Θ§―”≥ΛBAΒΫDΘ§ Ι![]() Θ§‘ρ
Θ§‘ρ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§άϊ”Ο»ΐΫ«–ΈΆβΫ«–‘÷ “ΉΒΟ
Θ§άϊ”Ο»ΐΫ«–ΈΆβΫ«–‘÷ “ΉΒΟ![]() Θ§Ής
Θ§Ής![]() ”ΎHΘ§…η
”ΎHΘ§…η![]() Θ§άϊ”ΟΚ§30Ε»»ΐ±ΏΒΡΙΊœΒΒΟΒΫ
Θ§άϊ”ΟΚ§30Ε»»ΐ±ΏΒΡΙΊœΒΒΟΒΫ![]() Θ§
Θ§![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() Θ§»ΜΚσ‘Ύ
Θ§»ΜΚσ‘Ύ![]() ÷–Θ§άϊ”Ο’ΐ«–ΒΡΕ®“εΩ…ΦΤΥψ≥ω
÷–Θ§άϊ”Ο’ΐ«–ΒΡΕ®“εΩ…ΦΤΥψ≥ω![]() Θ§Φ¥
Θ§Φ¥![]() Θ°
Θ°
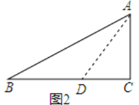
ΫβΘΚ»γΆΦ2Θ§…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§
Φ¥![]() ΘΜ
ΘΜ
Ι ¥πΑΗΈΣ![]() ΘΜ
ΘΜ![]() ΘΜ
ΘΜ
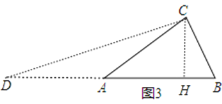
»γΆΦ3Θ§―”≥ΛBAΒΫDΘ§ Ι![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
Ής![]() ”ΎHΘ§…η
”ΎHΘ§…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§
Φ¥![]() Θ°
Θ°


 ”≈Β»…ζΧβΩβœΒΝ–¥πΑΗ
”≈Β»…ζΧβΩβœΒΝ–¥πΑΗ 53ΧλΧλΝΖœΒΝ–¥πΑΗ
53ΧλΧλΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
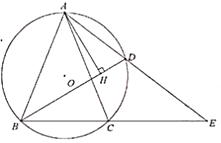
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABCΡΎΫ””ΎΓ―OΘ§![]() Θ§Βψ
Θ§Βψ![]() ΈΣ
ΈΣ![]() …œΒΡΕ·ΒψΘ§«“
…œΒΡΕ·ΒψΘ§«“![]() .
.
(1)«σ![]() ΒΡ≥ΛΕ»ΘΜ
ΒΡ≥ΛΕ»ΘΜ
(2)‘ΎΒψD‘ΥΕ·ΒΡΙΐ≥Χ÷–Θ§œ“ADΒΡ―”≥ΛœΏΫΜBCΒΡ―”≥ΛœΏ”ΎΒψEΘ§Έ ADAEΒΡ÷Β «Ζώ±δΜ·ΘΩ»τ≤Μ±δΘ§«κ«σ≥ωADAEΒΡ÷ΒΘΜ»τ±δΜ·Θ§«κΥΒΟςάμ”….
(3)‘ΎΒψDΒΡ‘ΥΕ·Ιΐ≥Χ÷–Θ§ΙΐAΒψΉςAHΓΆBDΘ§«σ÷ΛΘΚ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
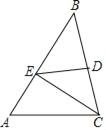
ΓΨΧβΡΩΓΩ“―÷Σ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœBΘΫ45ΓψΘ§ΒψD «BC±ΏΒΡ÷–ΒψΘ§DEΓΆBC”ΎΒψDΘ§ΫΜAB”ΎΒψEΘ§Ν§Ϋ”CEΘ°
Θ®1Θ©«σΓœAECΒΡΕ» ΐΘΜ
Θ®2Θ©«κΡψ≈–ΕœAEΓΔBEΓΔAC»ΐΧθœΏΕΈ÷°ΦδΒΡΒ»ΝΩΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœC=90ΓψΘ§“‘ACΈΣ÷±ΨΕΉςΓ―OΘ§ΫΜAB”ΎDΘ§ΙΐΒψOΉςOEΓΈABΘ§ΫΜBC”ΎEΘ°
Θ®1Θ©«σ÷ΛΘΚEDΈΣΓ―OΒΡ«–œΏΘΜ
Θ®2Θ©»γΙϊΓ―OΒΡΑκΨΕΈΣ![]() Θ§ED=2Θ§―”≥ΛEOΫΜΓ―O”ΎFΘ§Ν§Ϋ”DFΓΔAFΘ§«σΓςADFΒΡΟφΜΐΘ°
Θ§ED=2Θ§―”≥ΛEOΫΜΓ―O”ΎFΘ§Ν§Ϋ”DFΓΔAFΘ§«σΓςADFΒΡΟφΜΐΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©÷ΛΟςΦϊΫβΈωΘΜΘ®2Θ©![]()
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ© Ήœ»Ν§Ϋ”ODΘ§”…OEΓΈABΘ§ΗυΨίΤΫ––œΏ”κΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ Θ§“Ή÷ΛΒΟ![]() Γ’
Γ’![]() Φ¥Ω…ΒΟ
Φ¥Ω…ΒΟ![]() Θ§‘ρΩ…÷ΛΒΟ
Θ§‘ρΩ…÷ΛΒΟ![]() ΈΣ
ΈΣ![]() ΒΡ«–œΏΘΜ
ΒΡ«–œΏΘΜ
Θ®2Θ©Ν§Ϋ”CDΘ§ΗυΨί÷±ΨΕΥυΕ‘ΒΡ‘≤÷ήΫ« «÷±Ϋ«Θ§Φ¥Ω…ΒΟ![]() άϊ”ΟΙ¥Ι…Ε®άμΦ¥Ω…«σΒΟ
άϊ”ΟΙ¥Ι…Ε®άμΦ¥Ω…«σΒΟ![]() ΒΡ≥ΛΘ§”÷”…OEΓΈABΘ§÷ΛΒΟ
ΒΡ≥ΛΘ§”÷”…OEΓΈABΘ§÷ΛΒΟ![]() ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡΕ‘”Π±Ώ≥…±»άΐΘ§Φ¥Ω…«σΒΟ
ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡΕ‘”Π±Ώ≥…±»άΐΘ§Φ¥Ω…«σΒΟ![]() ΒΡ≥ΛΘ§»ΜΚσάϊ”Ο»ΐΫ«Κ· ΐΒΡ÷Σ ΕΘ§«σΒΟ
ΒΡ≥ΛΘ§»ΜΚσάϊ”Ο»ΐΫ«Κ· ΐΒΡ÷Σ ΕΘ§«σΒΟ![]() ”κ
”κ![]() ΒΡ≥ΛΘ§»ΜΚσάϊ”ΟSΓςADF=SΧί–ΈABEF-SΧί–ΈDBEF«σΒΟ¥πΑΗΘ°
ΒΡ≥ΛΘ§»ΜΚσάϊ”ΟSΓςADF=SΧί–ΈABEF-SΧί–ΈDBEF«σΒΟ¥πΑΗΘ°
‘ΧβΫβΈωΘΚ(1)÷ΛΟςΘΚΝ§Ϋ”ODΘ§

ÿOEøABȧ
ΓύΓœCOE=ΓœCADΘ§ΓœEOD=ΓœODAΘ§
ΓΏOA=OD,
ΓύΓœOAD=ΓœODAΘ§
ΓύΓœCOE=ΓœDOEΘ§
‘ΎΓςCOEΚΆΓςDOE÷–Θ§
 ΓύΓςCOEΓ’ΓςDOE(SAS)Θ§
ΓύΓςCOEΓ’ΓςDOE(SAS)Θ§
![]()
ΓύEDΓΆODΘ§
ΓύED «![]() ΒΡ«–œΏΘΜ
ΒΡ«–œΏΘΜ
(2)Ν§Ϋ”CDΘ§ΫΜOE”ΎMΘ§
‘ΎRtΓςODE÷–Θ§
ΓΏOD=32Θ§DE=2Θ§
![]()
ÿOEøABȧ
ΓύΓςCOEΓΉΓςCABΘ§
![]() ΓύAB=5Θ§
ΓύAB=5Θ§
ΓΏAC «÷±ΨΕΘ§
![]()
![]()
![]()
![]()
ÿEFøABȧ
![]()
![]()
![]()
ΓύSΓςADF=SΧί–ΈABEFSΧί–ΈDBEF
![]()
ΓύΓςADFΒΡΟφΜΐΈΣ![]()

ΓΨΧβ–ΆΓΩΫβ¥πΧβ
ΓΨΫα χΓΩ
25
ΓΨΧβΡΩΓΩΓΨΧβΡΩΓΩ“―÷ΣΘ§≈ΉΈοœΏy=ax2+ax+bΘ®aΓΌ0Θ©”κ÷±œΏy=2x+m”–“ΜΗωΙΪΙ≤ΒψMΘ®1Θ§0Θ©Θ§«“aΘΦbΘ°
Θ®1Θ©«σb”κaΒΡΙΊœΒ ΫΚΆ≈ΉΈοœΏΒΡΕΞΒψDΉχ±ξΘ®”ΟaΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
Θ®2Θ©÷±œΏ”κ≈ΉΈοœΏΒΡΝμΆβ“ΜΗωΫΜΒψΦ«ΈΣNΘ§«σΓςDMNΒΡΟφΜΐ”κaΒΡΙΊœΒ ΫΘΜ
Θ®3Θ©a=©¹1 ±Θ§÷±œΏy=©¹2x”κ≈ΉΈοœΏ‘ΎΒΎΕΰœσœόΫΜ”ΎΒψGΘ§ΒψGΓΔHΙΊ”Ύ‘≠ΒψΕ‘≥ΤΘ§œ÷ΫΪœΏΕΈGH―Ίy÷αœρ…œΤΫ“ΤtΗωΒΞΈΜΘ®tΘΨ0Θ©Θ§»τœΏΕΈGH”κ≈ΉΈοœΏ”–ΝΫΗω≤ΜΆ§ΒΡΙΪΙ≤ΒψΘ§ ‘«σtΒΡ»Γ÷ΒΖΕΈßΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏΒΡΕΞΒψΈΣCΘ®©¹1Θ§©¹1Θ©Θ§«“Ψ≠ΙΐΒψAΓΔΒψBΚΆΉχ±ξ‘≠ΒψOΘ§ΒψBΒΡΚαΉχ±ξΈΣ©¹3Θ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘ°
Θ®2Θ©«σΒψBΒΡΉχ±ξΦΑΓςBOCΒΡΟφΜΐΘ°
Θ®3Θ©»τΒψDΈΣ≈ΉΈοœΏ…œΒΡ“ΜΒψΘ§ΒψEΈΣΕ‘≥Τ÷α…œΒΡ“ΜΒψΘ§«““‘ΒψAΓΔOΓΔDΓΔEΈΣΕΞΒψΒΡΥΡ±Ώ–ΈΈΣΤΫ––ΥΡ±Ώ–ΈΘ§«κ‘ΎΉσ±ΏΒΡΆΦ…œ±ξ≥ωDΚΆEΒΡΈΜ÷ΟΘ§‘Ό÷±Ϋ”–¥≥ωΒψDΒΡΉχ±ξΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬Οφ≤ΡΝœΘΚ–ΓΟς―–ΨΩΝΥ’β―υ“ΜΗωΈ ΧβΘΚ«σ ΙΒΟΒ» Ϋ![]() ≥…ΝΔΒΡxΒΡΗω ΐΘ°–ΓΟςΖΔœ÷Θ§œ»ΫΪΗΟΒ» ΫΉΣΜ·ΈΣ
≥…ΝΔΒΡxΒΡΗω ΐΘ°–ΓΟςΖΔœ÷Θ§œ»ΫΪΗΟΒ» ΫΉΣΜ·ΈΣ![]() Θ§‘ΌΆ®Ιΐ―–ΨΩΚ· ΐ
Θ§‘ΌΆ®Ιΐ―–ΨΩΚ· ΐ![]() ΒΡΆΦœσ”κΚ· ΐ
ΒΡΆΦœσ”κΚ· ΐ![]() ΒΡΆΦœσΘ®»γΆΦΘ©ΒΡΫΜΒψΘ§ ΙΈ ΧβΒΟΒΫΫβΨωΘ°
ΒΡΆΦœσΘ®»γΆΦΘ©ΒΡΫΜΒψΘ§ ΙΈ ΧβΒΟΒΫΫβΨωΘ°
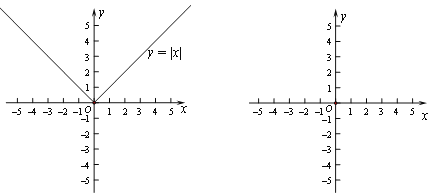
Θ®1Θ©Β±kΘΫ1 ±Θ§ ΙΒΟ‘≠Β» Ϋ≥…ΝΔΒΡxΒΡΗω ΐΈΣ_______ΘΜ
Θ®2Θ©Β±0ΘΦkΘΦ1 ±Θ§ ΙΒΟ‘≠Β» Ϋ≥…ΝΔΒΡxΒΡΗω ΐΈΣ_______ΘΜ
Θ®3Θ©Β±kΘΨ1 ±Θ§ ΙΒΟ‘≠Β» Ϋ≥…ΝΔΒΡxΒΡΗω ΐΈΣ_______Θ°
≤ΈΩΦ–ΓΟςΥΦΩΦΈ ΧβΒΡΖΫΖ®Θ§ΫβΨωΈ ΧβΘΚΙΊ”ΎxΒΡ≤ΜΒ» Ϋ![]() ÷Μ”–“ΜΗω’ϊ ΐΫβΘ§«σ
÷Μ”–“ΜΗω’ϊ ΐΫβΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
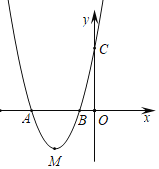
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏ![]() Ψ≠Ιΐ
Ψ≠Ιΐ![]() Θ§
Θ§![]() ΝΫΒψΘ°
ΝΫΒψΘ°
![]() «σ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
«σ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
![]() «σ≈ΉΈοœΏΒΡΕΞΒψΉχ±ξΘ§÷±Ϋ”–¥≥ωΒ±
«σ≈ΉΈοœΏΒΡΕΞΒψΉχ±ξΘ§÷±Ϋ”–¥≥ωΒ±![]() ±Θ§xΒΡ»Γ÷ΒΖΕΈßΘΜ
±Θ§xΒΡ»Γ÷ΒΖΕΈßΘΜ
![]() …ηΒψM «≈ΉΈοœΏΒΡΕΞΒψΘ§ ‘≈–Εœ≈ΉΈοœΏ…œ «Ζώ¥φ‘ΎΒψH¬ζΉψ
…ηΒψM «≈ΉΈοœΏΒΡΕΞΒψΘ§ ‘≈–Εœ≈ΉΈοœΏ…œ «Ζώ¥φ‘ΎΒψH¬ζΉψ![]() ΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψHΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψHΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚΙΐ![]() Άβ“ΜΒψCΉς
Άβ“ΜΒψCΉς![]() ÷±ΨΕAFΘ§¥ΙΉψΈΣEΘ§ΫΜœ“AB”ΎDΘ§»τ
÷±ΨΕAFΘ§¥ΙΉψΈΣEΘ§ΫΜœ“AB”ΎDΘ§»τ![]() Θ§‘ρ
Θ§‘ρ
![]() ≈–Εœ÷±œΏBC”κ
≈–Εœ÷±œΏBC”κ![]() ΒΡΈΜ÷ΟΙΊœΒΘ§≤Δ÷ΛΟςΘΜ
ΒΡΈΜ÷ΟΙΊœΒΘ§≤Δ÷ΛΟςΘΜ
![]() ΈΣOA÷–ΒψΘ§
ΈΣOA÷–ΒψΘ§![]() Θ§
Θ§![]() Θ§«κ÷±Ϋ”–¥≥ωΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°
Θ§«κ÷±Ϋ”–¥≥ωΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®12Ζ÷Θ©»γΆΦΥυ Ψ «ΥμΒάΒΡΫΊΟφ”…≈ΉΈοœΏΚΆ≥ΛΖΫ–ΈΙΙ≥…Θ§≥ΛΖΫ–ΈΒΡ≥Λ «12 mΘ§Ωμ «4 mΘ°Α¥’’ΆΦ÷–Υυ ΨΒΡ÷±Ϋ«Ήχ±ξœΒΘ§≈ΉΈοœΏΩ…“‘”Οy=![]() x2+bx+c±μ ΨΘ§«“≈ΉΈοœΏ…œΒΡΒψCΒΫOBΒΡΥ°ΤΫΨύάκΈΣ3 mΘ§ΒΫΒΊΟφOAΒΡΨύάκΈΣ
x2+bx+c±μ ΨΘ§«“≈ΉΈοœΏ…œΒΡΒψCΒΫOBΒΡΥ°ΤΫΨύάκΈΣ3 mΘ§ΒΫΒΊΟφOAΒΡΨύάκΈΣ![]() m.
m.
Θ®1Θ©«σ≈ΉΈοœΏΒΡΚ· ΐΙΊœΒ ΫΘ§≤ΔΦΤΥψ≥ωΙΑΕΞDΒΫΒΊΟφOAΒΡΨύάκΘΜ
Θ®2Θ©“ΜΝΨΜθ‘ΥΤϊ≥Β‘Ί“Μ≥ΛΖΫΧεΦ·ΉΑœδΚσΗΏΈΣ6mΘ§ΩμΈΣ4mΘ§»γΙϊΥμΒάΡΎ…ηΥΪœρ≥ΒΒάΘ§Ρ«Ο¥’βΝΨΜθ≥ΒΡήΖώΑ≤»ΪΆ®ΙΐΘΩ
Θ®3Θ©‘Ύ≈ΉΈοœΏ–ΆΙΑ±Ύ…œ–η“ΣΑ≤ΉΑΝΫ≈≈ΒΤΘ§ ΙΥϋΟ«άκΒΊΟφΒΡΗΏΕ»œύΒ»Θ§»γΙϊΒΤάκΒΊΟφΒΡΗΏΕ»≤Μ≥§Ιΐ8mΘ§Ρ«Ο¥ΝΫ≈≈ΒΤΒΡΥ°ΤΫΨύάκΉν–Γ «Εύ…ΌΟΉΘΩ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com