
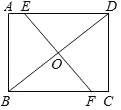
【题目】如图,在矩形ABCD中,EF经过对角线BD的中点O,分别交AD,BC于点E,F
(1)求证:△BOF≌△DOE;
(2)若AB=4cm,AD=5cm,当EF⊥BD时,求四边形ABFE的面积.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
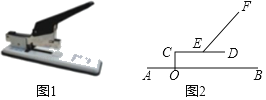
【题目】订书机是由推动器、托板、压形器、底座、定位轴等组成.如图1是一台放置在水平桌面上的大型订书机,将其侧面抽象成如图2所示的几何图形.若压形器EF的端点E固定于定位轴CD的中点处,在使用过程中,点D和点F随压形器及定位轴绕点C旋转,CO⊥AB于点O,CD=12cm连接CF,若∠FED=45°,∠FCD=30°.
(1)求FC的长;
(2)若OC=2cm求在使用过程中,当点D落在底座AB上时,请计算CD与AB的夹角及点F运动的路线之长.(结果精确到0.1cm,参考数据:sin9.6°≈0.17.π≈3.14,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点D为AC延长线上一点,连接BD,过A作
,点D为AC延长线上一点,连接BD,过A作![]() ,垂足为M,交BC于点N
,垂足为M,交BC于点N
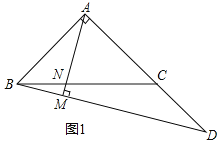
![]() 如图1,若
如图1,若![]() ,
,![]() ,求AM的长;
,求AM的长;
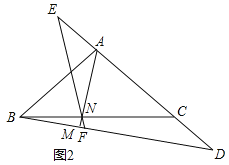
![]() 如图2,点E在CA的延长线上,且
如图2,点E在CA的延长线上,且![]() ,连接EN并延长交BD于点F,求证:
,连接EN并延长交BD于点F,求证:![]() ;
;
![]() 在
在![]() 的条件下,当
的条件下,当![]() 时,请求出
时,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
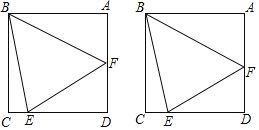
【题目】如图,边长为1的正方形ABCD中,点E、F分别在边CD、AD上,连接BE、BF、EF,且有AF+CE=EF.
(1)求(AF+1)(CE+1)的值;
(2)探究∠EBF的度数是否为定值,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】龙虾狂欢季再度开启,第![]() 届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为
届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为![]() 元,在整个销售旺季的
元,在整个销售旺季的![]() 天里,销售单价
天里,销售单价![]() 元/千克,与时间
元/千克,与时间![]() (天)之间的函数关系式为:
(天)之间的函数关系式为: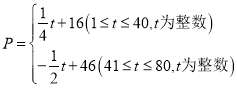 ,日销售量
,日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
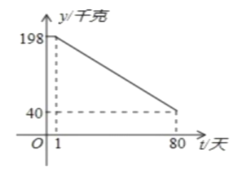
(1)求日销售量![]() 与时间
与时间![]() 的函数关系式?
的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前![]() 天中,该养殖户决定销售
天中,该养殖户决定销售![]() 千克小龙虾,就捐赠
千克小龙虾,就捐赠![]() 元给村里的特困户,在这前
元给村里的特困户,在这前![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若![]() 中,其中一个内角是另一个内角的一半,则称
中,其中一个内角是另一个内角的一半,则称![]() 为“半角三角形”.
为“半角三角形”.
(1)若![]() 为半角三角形,
为半角三角形,![]() ,则其余两个角的度数为 .
,则其余两个角的度数为 .
(2)如图1,在平行四边形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,以
上,以![]() 为折痕,将
为折痕,将![]() 向上翻折,点
向上翻折,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() ,若
,若![]() ,求证:
,求证:![]() 为半角三角形;
为半角三角形;
(3)如图2,以![]() 的边
的边![]() 为直径画圆,与边
为直径画圆,与边![]() 交于
交于![]() ,与边
,与边![]() 交于
交于![]() ,已知
,已知![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍.
倍.
①求证:![]() .
.
②若![]() 是半角三角形,
是半角三角形,![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,

(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①为汽车沿直线运动的速度v(m/s)与时间t(s)(0≤t≤40)之间的函数图象.根据对此图象的分析、理解,在图②中画出描述在这段时间内汽车离开出发点的路程s(m)与时间t(s)之间的函数图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
![]() 求出抛物线的对称轴方程以及与
求出抛物线的对称轴方程以及与![]() 轴的交点坐标
轴的交点坐标
![]() 当
当![]() 时,求出抛物线与
时,求出抛物线与![]() 轴的交点坐标
轴的交点坐标
![]() 已知
已知![]() 三点构成三角形
三点构成三角形![]() ,当抛物线与三角形
,当抛物线与三角形![]() 的三条边一共有
的三条边一共有![]() 个交点时,直接写出
个交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com