
【题目】龙虾狂欢季再度开启,第![]() 届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为
届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为![]() 元,在整个销售旺季的
元,在整个销售旺季的![]() 天里,销售单价
天里,销售单价![]() 元/千克,与时间
元/千克,与时间![]() (天)之间的函数关系式为:
(天)之间的函数关系式为: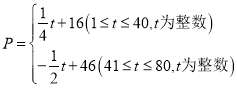 ,日销售量
,日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
(1)求日销售量![]() 与时间
与时间![]() 的函数关系式?
的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前![]() 天中,该养殖户决定销售
天中,该养殖户决定销售![]() 千克小龙虾,就捐赠
千克小龙虾,就捐赠![]() 元给村里的特困户,在这前
元给村里的特困户,在这前![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (
(![]() ,t为整数);(2)第
,t为整数);(2)第![]() 天的日销售利润最大,最大利润为
天的日销售利润最大,最大利润为![]() 元;(3)
元;(3)![]() .
.
【解析】
(1)设解析式为![]() ,根据图象得出点(1,198),(80,40)在该函数图象上,据此进一步代入求出
,根据图象得出点(1,198),(80,40)在该函数图象上,据此进一步代入求出![]() 的值,由此得出答案即可;
的值,由此得出答案即可;
(2)设日销售利润为![]() ,根据题意分①
,根据题意分①![]() 或
或![]() 两种情况进一步分析求解即可;
两种情况进一步分析求解即可;
(3)根据(2)中的等量关系得出函数解析式,进一步得出其对称轴,根据![]() 且销售利润随时间增大而增大,结合二次函数的性质进一步求解即可.
且销售利润随时间增大而增大,结合二次函数的性质进一步求解即可.
(1)设解析式为![]() 将(1,198),(80,40)代入得:
将(1,198),(80,40)代入得:
![]() ,
,
解得![]() ,
,
∴销售量![]() 与时间
与时间![]() 的函数关系式为:
的函数关系式为:![]() (
(![]() ,t为整数);
,t为整数);
(2)设日销售利润为![]() ,则
,则![]()
①![]() 时,
时,
![]() ,
,
∴当![]() 时,日销售利润为
时,日销售利润为![]() 取得最大值,且为2450;
取得最大值,且为2450;
②![]() 时,
时,
![]() ,
,
∴当![]() 时,日销售利润为
时,日销售利润为![]() 取得最大值,且为2301;
取得最大值,且为2301;
∵![]()
∴第![]() 天的日销售利润最大,最大利润为
天的日销售利润最大,最大利润为![]() 元;
元;
(3)设日销售利润为![]() ,根据题意得:
,根据题意得:
![]() ,
,
∴该函数图像的对称轴为![]() ,
,
∵![]() 随
随![]() 的增大而增大,且
的增大而增大,且![]()
∴由二次函数的图象及性质可知,![]() ,
,
解得:![]() ,
,
又∵![]() ,
,
∴![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 是坐标原点,四边形
是坐标原点,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
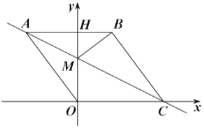
(Ⅰ)求直线![]() 的解析式;
的解析式;
(Ⅱ)动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以2个单位/秒的速度向终点
方向以2个单位/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]()
![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
①当![]() 时,求
时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
②在点![]() 运动过程中,当
运动过程中,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的教室A位于工地O的正西方向,且OA=200m,一台拖拉机从O点出发,以每秒5m的速度沿北偏西53°的方向行驶,设拖拉机的噪声污染半径为130m,则教室A是否在拖拉机的噪声污染范围内?若不在,请说明理由;若在,求出教室A受噪声污染的时间有几秒.(参考数据:sin53°≈0.80,sin37°≈0.60,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱乐器),现将收集到的数据绘制如下的两幅不完整的统计图.
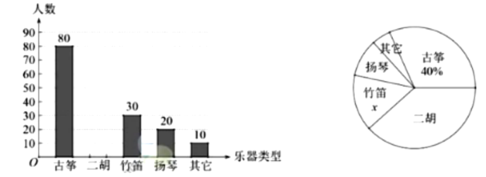
(1)这次共抽取 学生进行调查,扇形统计图中的![]() .
.
(2)请补全统计图;
(3)在扇形统计图中“扬琴”所对扇形的圆心角是 度;
(4)若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有 名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请仅用无刻度直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图1,在![]() 的正方形网格中,每个小正方形的边长为1,小正方形的顶点叫做格点.
的正方形网格中,每个小正方形的边长为1,小正方形的顶点叫做格点.![]() 的顶点在格点上,过点
的顶点在格点上,过点![]() 画一条直线平分
画一条直线平分![]() 的面积;
的面积;
(2)如图2,点![]() 在正方形
在正方形![]() 的内部,且
的内部,且![]() ,过点
,过点![]() 画一条射线平分
画一条射线平分![]() ;
;
(3)如图3,点![]() 、
、![]() 、
、![]() 均在
均在![]() 上,且
上,且![]() ,在优弧
,在优弧![]() 上画
上画![]() 、
、![]() 两点,使
两点,使![]() .
.
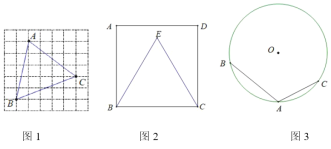
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(探究发现)
如图1,![]() 的顶点
的顶点![]() 在正方形
在正方形![]() 两条对角线的交点处,
两条对角线的交点处,![]() ,将
,将![]() 绕点
绕点![]() 旋转,旋转过程中,
旋转,旋转过程中,![]() 的两边分别与正方形
的两边分别与正方形![]() 的边
的边![]() 和
和![]() 交于点
交于点![]() 和点
和点![]() (点
(点![]() 与点
与点![]() ,
,![]() 不重合).则
不重合).则![]() 之间满足的数量关系是 .
之间满足的数量关系是 .
(2)(类比应用)
如图2,若将(1)中的“正方形![]() ”改为“
”改为“![]() 的菱形
的菱形![]() ”,其他条件不变,当
”,其他条件不变,当![]() 时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
(3)(拓展延伸)
如图3,![]() ,
,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() ,且
,且![]() ,点
,点![]() 是
是![]() 上一点,
上一点,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com