
【题目】如图,某校教学楼![]() 与实验楼
与实验楼![]() 的水平间距
的水平间距![]() 米,在实验楼顶部
米,在实验楼顶部![]() 点测得教学楼顶部
点测得教学楼顶部![]() 点的仰角是
点的仰角是![]() ,底部
,底部![]() 点的俯角是
点的俯角是![]() ,则教学楼
,则教学楼![]() 的高度是____米(结果保留根号).
的高度是____米(结果保留根号).
【答案】(15+15![]() )
)
【解析】
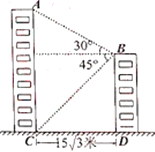
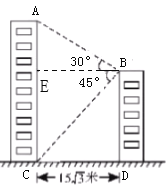
过点B作BM⊥AC,垂足为E,则∠ABE=30°,∠CBE=45°,四边形CDBE是矩形,继而证明∠CEB=∠CBE,从而可得CE长,在Rt△ABE中,利用tan∠ABE=![]() ,求出AE长,继而可得AC长.
,求出AE长,继而可得AC长.
过点B作BM⊥AC,垂足为E,
则∠ABE=30°,∠CBE=45°,四边形CDBE是矩形,
∴BE=CD=15![]() ,
,
∵∠CEB=90°,
∴∠CEB=90°-∠CBE=45°=∠CBE,
∴CE=BE=15![]() ,
,
在Rt△ABE中,tan∠ABE=![]() ,
,
即![]() ,
,
∴AE=15,
∴AC=AE+CE=15+15![]() ,
,
即教学楼AC的高度是(15+15![]() )米,
)米,
故答案为:(15+15![]() ).
).


科目:初中数学 来源: 题型:
【题目】阅读理解:
类比定义:我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则等等.小学里,把分子比分母小的分数叫做真分数,类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.
拓展定义:
对于任何一个分式都可以化成整式与真分式的和的形式,
如:![]() ;
;
![]() .
.
理解定义:
(1)下列分式中,属于真分式的是:____属于假分式的是:_____(填序号)
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
拓展应用:
(2)将分式![]() 化成整式与真分式的和的形式;
化成整式与真分式的和的形式;
(3)将假分式![]() 化成整式与真分式的和的形式。
化成整式与真分式的和的形式。
查看答案和解析>>
科目:初中数学 来源: 题型:
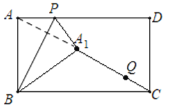
【题目】如图,在矩形ABCD中,![]() ,AD=9,点P是AD边上的一个动点,连接BP,将矩形ABCD沿BP折叠,得到△A1PB,连接A1C,取A1C的三等分点Q(CQ<A1Q),当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( )
,AD=9,点P是AD边上的一个动点,连接BP,将矩形ABCD沿BP折叠,得到△A1PB,连接A1C,取A1C的三等分点Q(CQ<A1Q),当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( )
A.πB.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】龙虾狂欢季再度开启,第![]() 届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为
届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为![]() 元,在整个销售旺季的
元,在整个销售旺季的![]() 天里,销售单价
天里,销售单价![]() 元/千克,与时间
元/千克,与时间![]() (天)之间的函数关系式为:
(天)之间的函数关系式为: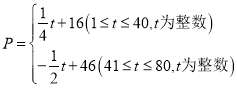 ,日销售量
,日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
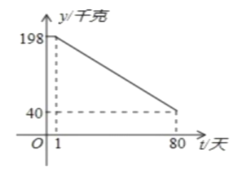
(1)求日销售量![]() 与时间
与时间![]() 的函数关系式?
的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前![]() 天中,该养殖户决定销售
天中,该养殖户决定销售![]() 千克小龙虾,就捐赠
千克小龙虾,就捐赠![]() 元给村里的特困户,在这前
元给村里的特困户,在这前![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,D,E,F分别是AB,BC,AC的中点,连结DF,EF,BF.
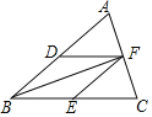
(1)求证:四边形BEFD是平行四边形;
(2)若∠AFB=90°,AB=4,求四边形BEFD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=a(x+2)2﹣3与y2=![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=![]() ;③当x=0时,y2﹣y1=6;④AB+AC=10;其中正确结论的个数是( )
;③当x=0时,y2﹣y1=6;④AB+AC=10;其中正确结论的个数是( )
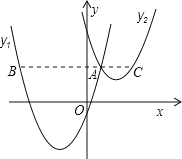
A.①②④B.①③④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投掷一次骰子,向上一面的点数记为![]() ,再投掷一次骰子,向上一面的点数记为
,再投掷一次骰子,向上一面的点数记为![]() ,这样就确定点
,这样就确定点![]() 的一个坐标
的一个坐标![]() ,那么点
,那么点![]() 落在双曲线
落在双曲线![]() 上的概率为( )
上的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△DEF均为等腰直角三角形,AB=2,DE=1,E、B、F、C在同一条直线上,开始时点B与点F重合,让△DEF沿直线BC向右移动,最后点C与点E重合,设两三角形重合面积为y,点F移动的距离为x,则y关于x的大致图象是( )

A.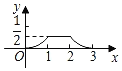 B.
B.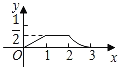
C.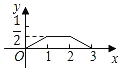 D.
D.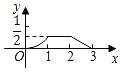
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com