
【题目】已知四边形ABCD是⊙O的内接梯形,AB∥CD,AB=8cm,CD=6cm,⊙O的半径是5cm,则梯形的面积是_____cm2.
【答案】49或7
【解析】
梯形的高就是弦AB与CD之间的距离,根据垂径定理求得两弦的弦心距,当CD与AB在圆心的同侧时,梯形的高等于两弦心距的差,当CD与AB在圆心的两侧时,梯形的高等于两弦心距的和,根据梯形的面积公式即可求解.
解:过点O作OE⊥CE于点E,交AB于点F,连接OA,OC,
∵AB=8,CD=6,
∴CE![]() BC
BC![]() 6=3,AF
6=3,AF![]() AB
AB![]() 8=4,
8=4,
在Rt△COE中,OE![]() 4;
4;
在Rt△AOF中,OF![]() 3,
3,
当点AB,CD在圆心O的同侧时,如图1所示:
EF=OE+OF=4+3=7,S梯形ABCD![]() (AB+CD)EF
(AB+CD)EF![]() (6+8)×7=49;
(6+8)×7=49;
当点AB,CD在圆心O的异侧时,如图2所示:
EF=OE﹣OF=4﹣3=1,S梯形ABCD![]() (AB+CD)EF
(AB+CD)EF![]() (6+8)×1=7;
(6+8)×1=7;
∴梯形ABCD的面积为:7cm2或49cm2.
故答案为:7cm2或49cm2.



 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
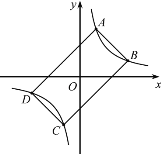
【题目】如图,已知矩形ABCD的四个顶点都在双曲线y=![]() (k>0)上,BC=2AB,且矩形ABCD的面积是32,则k的值是( )
(k>0)上,BC=2AB,且矩形ABCD的面积是32,则k的值是( )
A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①若![]() 则
则![]() ②若
②若![]() 则
则![]() ③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )
③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
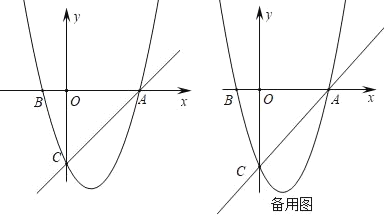
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
(1)求抛物线的解析式;
(2)若动点P在第四象限内的抛物线上,过动点P作x轴的垂线交直线AC于点D,交x轴于点E,垂足为E,求线段PD的长,当线段PD最长时,求出点P的坐标;
(3)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
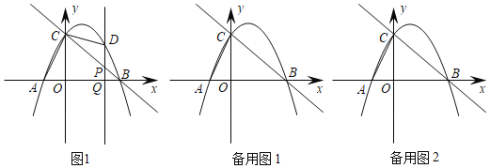
【题目】如图所示,平面直角坐标系中,直线y=﹣x+3交坐标轴与B、C两点,抛物线y=ax2+bx+3经过B、C两点,且交x轴于另一点A(﹣1,0).点D为抛物线在第一象限内的一点,过点D作DQ∥CO,DQ交BC于点P,交x轴于点Q.
(1)求抛物线解析式;
(2)设点P的横坐标为m,在点D的移动过程中,存在∠DCP=∠ACO,求出m值;
(3)在抛物线取点E,在坐标系内取点F,问是否存在以C、B、E、F为顶点且以CB为边的矩形?如果有请求出点E的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com