
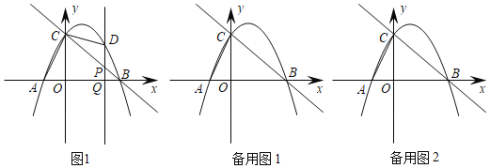
【题目】如图所示,平面直角坐标系中,直线y=﹣x+3交坐标轴与B、C两点,抛物线y=ax2+bx+3经过B、C两点,且交x轴于另一点A(﹣1,0).点D为抛物线在第一象限内的一点,过点D作DQ∥CO,DQ交BC于点P,交x轴于点Q.
(1)求抛物线解析式;
(2)设点P的横坐标为m,在点D的移动过程中,存在∠DCP=∠ACO,求出m值;
(3)在抛物线取点E,在坐标系内取点F,问是否存在以C、B、E、F为顶点且以CB为边的矩形?如果有请求出点E的坐标;如果不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)m=![]() ;(3)存在,当点E(1,4)或(﹣2,﹣5)时,以C、B、E、F为顶点且以CB为边的矩形.
;(3)存在,当点E(1,4)或(﹣2,﹣5)时,以C、B、E、F为顶点且以CB为边的矩形.
【解析】
(1)利用一次函数与坐标轴相交,求出B、C两点的坐标,利用待定系数法求出二次函数解析式;
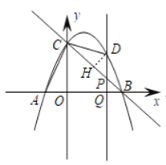
(2)如图,过点D作DH⊥BC于H,点![]() ,点
,点![]() ,利用参数求出DH,CH的长,由锐角三角函数可求解;
,利用参数求出DH,CH的长,由锐角三角函数可求解;
(3)分两种情况讨论,求出直线CE的方程或BE的方程,联立方程组可求解.
(1)∵直线y=﹣x+3交坐标轴与B、C两点,
∴点B(3,0),点C(0,3),
∵抛物线![]() 经过B、C两点,且交x轴于另一点A(﹣1,0),
经过B、C两点,且交x轴于另一点A(﹣1,0),
∴![]()
解得:![]()
∴抛物线解析式为:![]() ;
;
(2)如图,过点D作DH⊥BC于H,
∵点B(3,0),点C(0,3),点A(﹣1,0),
∴CO=3=BO,AO=1,
∴∠BCO=∠CBO=45°,BC=3![]() ,
,
∵DQ⊥OB,
∴∠BPQ=∠PBQ=45°,
∴PQ=QB,BP=![]() PQ,
PQ,
∵点P的横坐标为m,
∴点![]() ,点
,点![]() ,
,
∴PQ=﹣m+3,![]() ,
,
∴![]() ,BP=
,BP=![]() (﹣m+3)
(﹣m+3)
∵∠DPH=∠BPQ=45°,DH⊥BC,
∴∠HDP=∠DPH=45°,
∴DH=PH=![]()
![]() ,
,
∴CH=3![]() ﹣
﹣![]() (﹣m+3)﹣
(﹣m+3)﹣![]()
![]() =
=![]()
![]() ,
,
∵∠DCP=∠ACO,
∴tan∠DCP=tan∠ACO=![]() ,
,
∴![]() =
=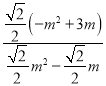
∴m=0(舍去),m=![]() ;
;
(3)存在,
若CE⊥BC时,
直线CE解析式为:y=x+3,
∴![]()
∴![]() (舍去),
(舍去),![]()
∴点E坐标![]() ,
,
若BE⊥BC时,
直线BE解析式为:y=x﹣3,
∴![]()
∴![]() (舍去),
(舍去),![]()
∴点E坐标![]() ,
,
综上所述:当点![]() 或
或![]() 时,以C、B、E、F为顶点且以CB为边的矩形.
时,以C、B、E、F为顶点且以CB为边的矩形.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
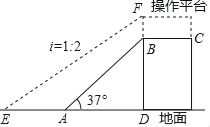
【题目】如图,为了将货物装入大型的集装箱卡车,需要利用传送带AB将货物从地面传送到高1.8米(即BD=1.8米)的操作平台BC上.已知传送带AB与地面所成斜坡的坡角∠BAD=37°.
(1)求传送带AB的长度;
(2)因实际需要,现在操作平台和传送带进行改造,如图中虚线所示,操作平台加高0.2米(即BF=0.2米),传送带与地面所成斜坡的坡度i=1:2.求改造后传送带EF的长度.(精确到0.1米)(参考数值:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ![]() ≈1.41,
≈1.41, ![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
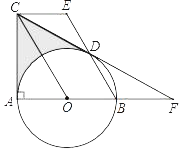
【题目】如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=8,求图中阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
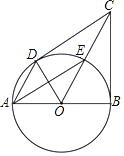
【题目】如图,已知D是⊙O上一点,AB是直径,∠BAD的平分线交⊙O于点E,⊙O的切线BC交OE的延长线于点C,连接OD,CD.
(1)求证:CD⊥OD.
(2)若AB=2,填空:
①当CE= 时,四边形BCDO是正方形.
②作△AEO关于直线OE对称的△FEO,连接BF,BE,当四边形BEOF是菱形时,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
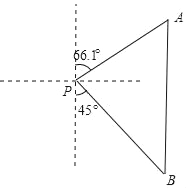
【题目】如图,一艘海轮位于灯塔P的北偏东66.1°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求BP和BA的长(结果取整数).
参考数据:sin66.1°≈0.91,cos66.1°≈0.41,tan64°≈2.26,![]() 取1.414.
取1.414.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
类比定义:我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则等等.小学里,把分子比分母小的分数叫做真分数,类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.
拓展定义:
对于任何一个分式都可以化成整式与真分式的和的形式,
如:![]() ;
;
![]() .
.
理解定义:
(1)下列分式中,属于真分式的是:____属于假分式的是:_____(填序号)
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
拓展应用:
(2)将分式![]() 化成整式与真分式的和的形式;
化成整式与真分式的和的形式;
(3)将假分式![]() 化成整式与真分式的和的形式。
化成整式与真分式的和的形式。
查看答案和解析>>
科目:初中数学 来源: 题型:
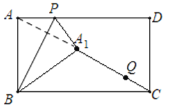
【题目】如图,在矩形ABCD中,![]() ,AD=9,点P是AD边上的一个动点,连接BP,将矩形ABCD沿BP折叠,得到△A1PB,连接A1C,取A1C的三等分点Q(CQ<A1Q),当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( )
,AD=9,点P是AD边上的一个动点,连接BP,将矩形ABCD沿BP折叠,得到△A1PB,连接A1C,取A1C的三等分点Q(CQ<A1Q),当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( )
A.πB.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投掷一次骰子,向上一面的点数记为![]() ,再投掷一次骰子,向上一面的点数记为
,再投掷一次骰子,向上一面的点数记为![]() ,这样就确定点
,这样就确定点![]() 的一个坐标
的一个坐标![]() ,那么点
,那么点![]() 落在双曲线
落在双曲线![]() 上的概率为( )
上的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com