
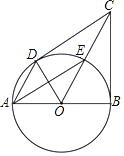
【题目】如图,已知D是⊙O上一点,AB是直径,∠BAD的平分线交⊙O于点E,⊙O的切线BC交OE的延长线于点C,连接OD,CD.
(1)求证:CD⊥OD.
(2)若AB=2,填空:
①当CE= 时,四边形BCDO是正方形.
②作△AEO关于直线OE对称的△FEO,连接BF,BE,当四边形BEOF是菱形时,求CE的长.
【答案】(1)见解析;(2)①![]() ﹣1;②CE=1.
﹣1;②CE=1.
【解析】
(1)证出∠DAE=∠OEA,得出![]() ,由圆周角定理证出∠BOC=∠BAD=∠DOC,证明△ODC≌△OBC(SAS),得出∠ODC=∠OBC=90°,即可得出结论;
,由圆周角定理证出∠BOC=∠BAD=∠DOC,证明△ODC≌△OBC(SAS),得出∠ODC=∠OBC=90°,即可得出结论;
(2)①求出![]() ,由(1)得∠OBC=90°,△ODC≌△OBC,由勾股定理得出
,由(1)得∠OBC=90°,△ODC≌△OBC,由勾股定理得出![]() ,得出OB=BC=DC=OD,证出四边形BCDO是菱形,由∠OBC=90°,即可得出结论;
,得出OB=BC=DC=OD,证出四边形BCDO是菱形,由∠OBC=90°,即可得出结论;
②由菱形的性质得出BE=OE=1,得出∠EOB=∠EBO,证出∠BCE=∠CBE,即可得出CE=BE=1.
(1)∵BC是⊙O的切线,
∴BC⊥OB,
∴∠OBC=90°,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵OA=OE,
∴∠BAE=∠OEA,
∴∠DAE=∠OEA,
∴![]() ,
,
∴∠BOC=∠BAD,
∵∠BOD=∠BOC+∠DOC=2∠BAD,
∴∠BOC=∠BAD=∠DOC,
在△ODC和△OBC中,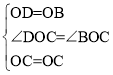 ,
,
∴△ODC≌△OBC(SAS),
∴∠ODC=∠OBC=90°,
∴CD⊥OD;
(2)①当CE=![]() ﹣1时,四边形BCDO是正方形;理由如下:
﹣1时,四边形BCDO是正方形;理由如下:
∵AB=2,
∴OB=OE=OD=1,
∴OC=OE+CE=![]() ,
,
由(1)得:∠OBC=90°,△ODC≌△OBC,
∴DC=BC=![]() =
=![]() =1,
=1,
∴OB=BC=DC=OD,
∴四边形BCDO是菱形,
∵∠OBC=90°,
∴四边形BCDO是正方形;
故答案为:![]() ﹣1;
﹣1;
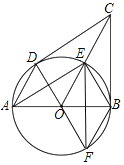
②如图所示:
∵△AEO与△FEO关于直线OE对称,
∴OF=OA,
∴F在⊙O上,
∵四边形BEOF是菱形,
∴BE=OE=1,
∴∠EOB=∠EBO,
∵∠EOB+∠BCE=90°,∠EBO+∠CBE=90°,
∴∠BCE=∠CBE,
∴CE=BE=1.


科目:初中数学 来源: 题型:
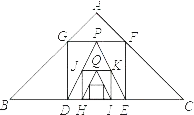
【题目】如图,已知在Rt△ABC中,AB=AC=3![]() ,在△ABC内作第1个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第2个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第3个内接正方形…,依次进行下去,则第2019个内接正方形的边长为_____.
,在△ABC内作第1个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第2个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第3个内接正方形…,依次进行下去,则第2019个内接正方形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B,DE交AC于点E.
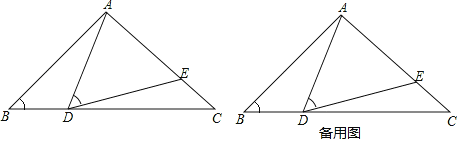
(1)求证:△ABD∽△DCE;
(2)若△DCE为直角三角形,求BD.
(3)若以AE为直径的圆与边BC相切,求AD;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标系中,直线y=﹣x+3交坐标轴与B、C两点,抛物线y=ax2+bx+3经过B、C两点,且交x轴于另一点A(﹣1,0).点D为抛物线在第一象限内的一点,过点D作DQ∥CO,DQ交BC于点P,交x轴于点Q.
(1)求抛物线解析式;
(2)设点P的横坐标为m,在点D的移动过程中,存在∠DCP=∠ACO,求出m值;
(3)在抛物线取点E,在坐标系内取点F,问是否存在以C、B、E、F为顶点且以CB为边的矩形?如果有请求出点E的坐标;如果不存在,请说明理由.
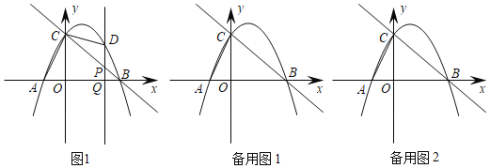
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 是坐标原点,四边形
是坐标原点,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
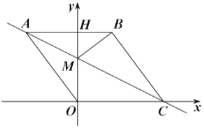
(Ⅰ)求直线![]() 的解析式;
的解析式;
(Ⅱ)动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以2个单位/秒的速度向终点
方向以2个单位/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]()
![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
①当![]() 时,求
时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
②在点![]() 运动过程中,当
运动过程中,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的教室A位于工地O的正西方向,且OA=200m,一台拖拉机从O点出发,以每秒5m的速度沿北偏西53°的方向行驶,设拖拉机的噪声污染半径为130m,则教室A是否在拖拉机的噪声污染范围内?若不在,请说明理由;若在,求出教室A受噪声污染的时间有几秒.(参考数据:sin53°≈0.80,sin37°≈0.60,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
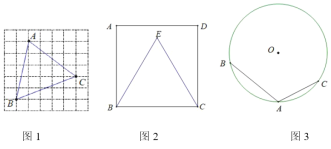
【题目】请仅用无刻度直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图1,在![]() 的正方形网格中,每个小正方形的边长为1,小正方形的顶点叫做格点.
的正方形网格中,每个小正方形的边长为1,小正方形的顶点叫做格点.![]() 的顶点在格点上,过点
的顶点在格点上,过点![]() 画一条直线平分
画一条直线平分![]() 的面积;
的面积;
(2)如图2,点![]() 在正方形
在正方形![]() 的内部,且
的内部,且![]() ,过点
,过点![]() 画一条射线平分
画一条射线平分![]() ;
;
(3)如图3,点![]() 、
、![]() 、
、![]() 均在
均在![]() 上,且
上,且![]() ,在优弧
,在优弧![]() 上画
上画![]() 、
、![]() 两点,使
两点,使![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com