
【题目】如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B,DE交AC于点E.
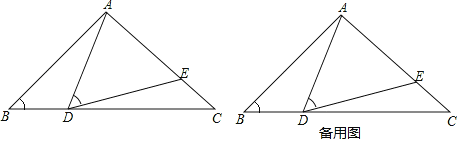
(1)求证:△ABD∽△DCE;
(2)若△DCE为直角三角形,求BD.
(3)若以AE为直径的圆与边BC相切,求AD;
【答案】(1)见解析;(2)BD=8或![]() ;(3)5
;(3)5![]()
【解析】
(1)证明∠ADB=∠DEC,即可得出结论;
(2)过点A作AG⊥BC于G,分两种情况讨论,当∠AED=90°时,当∠CDE=90°时通过三角形相似即可求得;
(3)取AE的中点O,过O作OF⊥BC于F,设BD=x,AE=y,可分别表示OA和OC,由OF∥AG,得出![]() ,得出关于x的方程,解出x即可求出DG长,则AD长可求出.
,得出关于x的方程,解出x即可求出DG长,则AD长可求出.
(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠B,
∴∠ADE=∠C,
∵∠ADB=180°﹣∠ADE﹣∠CDE,∠DEC=180°﹣∠C﹣∠CDE,
∴∠ADB=∠DEC,
∵∠B=∠C,
∴△ABD∽△DCE;
(2)解:如图1,过点A作AG⊥BC于G,

∴CG=![]() BC=8,
BC=8,
∴AG=![]() =6,
=6,
设∠ADE=∠B=∠C=α
∴cosα=![]() ,
,
当∠AED=90°时,
∵AB=AC,
∴∠B=∠C,
又∵∠ADE=∠B
∴∠ADE=∠C,
∴△ADE∽△ACD,
∵∠AED=90°,
∴∠ADC=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴BD=8.
当∠CDE=90°时,由(1)知△CDE∽△BAD,
∵∠CDE=90°,
∴∠BAD=90°,
∵cosα=![]() .AB=10,
.AB=10,
∴cosB=![]() ,
,
∴BD=![]() .
.
即:BD=8或![]() .
.
(3)解:如图2,取AE的中点O,过O作OF⊥BC于F,

设BD=x,AE=y,
∴CD=BC﹣BD=16﹣x,CE=AC﹣AE=10﹣y,
由(1)知,△ABD∽△DCE,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴OA=![]() ,
,
∴OC=AC﹣OA
=10﹣![]()
![]() ,
,
∵以AE为直径的圆与边BC相切,
∴OF=OA=![]() ,
,
∵AG⊥BC,OF⊥BC,
∴OF∥AG,
∴![]() ,
,
∴OCAG=OFAC,
∴![]() ,
,
∴x=8+![]() 或x=8﹣
或x=8﹣![]() ,
,
∴DG=![]() ,
,
在Rt△AGD中,根据勾股定理得,AD=![]() =5
=5![]() .
.


科目:初中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 与
与![]() 成反比例
成反比例![]() 与
与![]() 成正比例,函数的自变量
成正比例,函数的自变量![]() 的取值范围是
的取值范围是![]() ,且当
,且当![]() 或
或![]() 时,
时,![]() 的值均为
的值均为![]() 。
。
请对该函数及其图象进行如下探究:
(1)解析式探究:根据给定的条件,可以确定出该函数的解析式为: .
(2)函数图象探宄:①根据解析式,选取适当的自变量![]() ,并完成下表:
,并完成下表:
|
| ... | ||||||||
| ... |
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出函数图象.
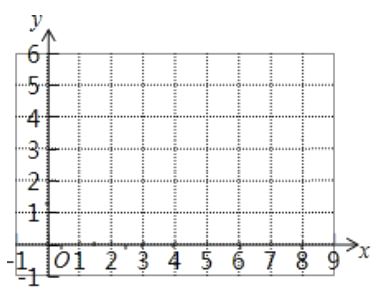
(3)结合画出的函数图象,解决问题:
①当![]() ,
,![]() ,
,![]() 时,函数值分别为
时,函数值分别为![]() ,则
,则![]() 的大小关系为: (用“
的大小关系为: (用“![]() ”或“
”或“![]() ”表示)
”表示)
②若直线![]() 与该函数图象有两个交点,则
与该函数图象有两个交点,则![]() 的取值范围是 ,此时,
的取值范围是 ,此时,![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
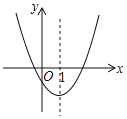
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac; ②4a+2b+c<0;③不等式ax2+bx+c>0的解集是x≥3.5;④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.上述4个判断中,正确的是( )
A.①②B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=60°,半径为2![]() 的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为____.
的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=60°,半径为2![]() 的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为____.
的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为____.
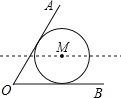
查看答案和解析>>
科目:初中数学 来源: 题型:
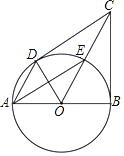
【题目】如图,已知D是⊙O上一点,AB是直径,∠BAD的平分线交⊙O于点E,⊙O的切线BC交OE的延长线于点C,连接OD,CD.
(1)求证:CD⊥OD.
(2)若AB=2,填空:
①当CE= 时,四边形BCDO是正方形.
②作△AEO关于直线OE对称的△FEO,连接BF,BE,当四边形BEOF是菱形时,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长度等于_____;
(Ⅱ)在图中有一点P,若连接AP,PB,PC,满足AP平分∠A,且PC=PB,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
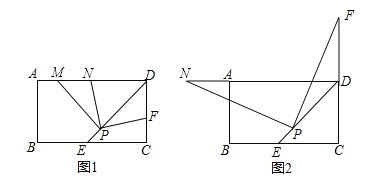
【题目】矩形ABCD中,DE平分∠ADC交BC边于点E,P为DE上的一点(PE<PD),PM⊥PD,PM交AD边于点M.
(1)若点F是边CD上一点,满足PF⊥PN,且点N位于AD边上,如图1所示.
求证:①PN=PF;②DF+DN=![]() DP;
DP;
(2)如图2所示,当点F在CD边的延长线上时,仍然满足PF⊥PN,此时点N位于DA边的延长线上,如图2所示;试问DF,DN,DP有怎样的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 两点在反比例函数
两点在反比例函数![]() 的图象上,下列三个命题:①若
的图象上,下列三个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,
,![]() ,则
,则![]() ;③过
;③过![]() 、
、![]() 两点的直线与
两点的直线与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() ,则
,则![]() .其中真命题个数是( )
.其中真命题个数是( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com