
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac; ②4a+2b+c<0;③不等式ax2+bx+c>0的解集是x≥3.5;④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.上述4个判断中,正确的是( )
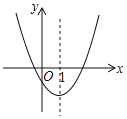
A.①②B.①②④C.①③④D.②③④
【答案】B
【解析】
①根据抛物线与x轴有交点,即可判定正确;
②由图象可知,x=2时,y<0,即可判定正确;
③错误,不等式![]() 的解集是
的解集是![]() 或
或![]() (
(![]() ,
,![]() 分别为抛物线与x轴解得的横坐标,
分别为抛物线与x轴解得的横坐标,![]() 是左交点横坐标);
是左交点横坐标);
④根据点(5,![]() )到对称轴的距离比点(-2,
)到对称轴的距离比点(-2,![]() )到对称轴的距离大,即可判定正确.
)到对称轴的距离大,即可判定正确.
解:∵抛物线与x轴有两个交点,
∴![]() ,
,
∴![]() ,故①正确,
,故①正确,
由图象可知,x=2时,y<0,
∴4a=2b+c<0,故②正确,
由图象可知,不等式ax2+bx+c>0的解集是![]() 或
或![]() (
(![]() ,
,![]() 分别为抛物线与x轴交点的横坐标,
分别为抛物线与x轴交点的横坐标,![]() 是左交点横坐标),故③错误,
是左交点横坐标),故③错误,
由图象可知,点(5,![]() )到对称轴的距离比点(-2,
)到对称轴的距离比点(-2,![]() )到对称轴的距离大,
)到对称轴的距离大,
∴y2>y1,故④正确.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数![]() 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )

A.3 B.4 C.6 D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=50°,连接BD,CE交于点F.填空:
①的值为 ;②∠BFC的度数为 .
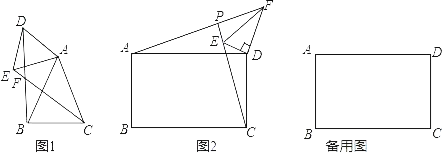
(2)类比探究
如图2,在矩形ABCD和△DEF中,AD=![]() AB,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点P.求
AB,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点P.求![]() 的值及∠APC的度数,并说明理由;
的值及∠APC的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△DEF绕点D在平面内旋装,AF,CE所在直线交于点P,若DF=![]() ,AB=
,AB=![]() ,求出当点P与点E重合时AF的长.
,求出当点P与点E重合时AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在⊙O中,AB是直径,弦EF∥AB,在直径AB下方的半圆上有一个定点H(点H不与点A,B重合),请仅用无刻度的直尺画出劣弧![]() 的中点P,并在直线AB上画出点G,使直线AB平分∠HGP.(保留作图痕迹,不写作法)
的中点P,并在直线AB上画出点G,使直线AB平分∠HGP.(保留作图痕迹,不写作法)


(2)尺规作图:如图2,已知线段a、c,请你用两种不同的方法作Rt△ABC,使其斜边AB=c,一条直角边BC=a.(保留作图痕迹,不写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元、40元,商场销售4台A型号和2台B型号计算器,可获利润80元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)求商场销售A、B两种型号计算器的销售价格分别是多少元?
(2)商场准备用不多于2500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别标有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)若规定两个数字的积为偶数时甲赢,两个数字的积为奇数时乙赢,请问这个游戏对甲、乙两人是否公平?
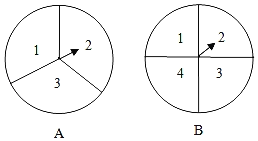
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B,DE交AC于点E.
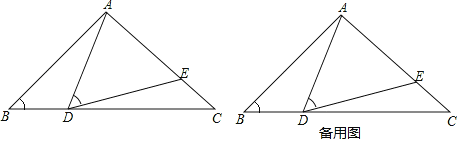
(1)求证:△ABD∽△DCE;
(2)若△DCE为直角三角形,求BD.
(3)若以AE为直径的圆与边BC相切,求AD;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com