
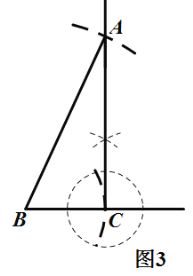
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌдкЁбOжаЃЌABЪЧжБОЖЃЌЯвEFЁЮABЃЌдкжБОЖABЯТЗНЕФАыдВЩЯгавЛИіЖЈЕуHЃЈЕуHВЛгыЕуAЃЌBжиКЯЃЉЃЌЧыНігУЮоПЬЖШЕФжБГпЛГіСгЛЁ![]() ЕФжаЕуPЃЌВЂдкжБЯпABЩЯЛГіЕуGЃЌЪЙжБЯпABЦНЗжЁЯHGPЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉ
ЕФжаЕуPЃЌВЂдкжБЯпABЩЯЛГіЕуGЃЌЪЙжБЯпABЦНЗжЁЯHGPЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉ
 ЁЁЁЁЁЁЁЁ
ЁЁЁЁЁЁЁЁ
ЃЈ2ЃЉГпЙцзїЭМЃКШчЭМ2ЃЌвбжЊЯпЖЮaЁЂcЃЌЧыФугУСНжжВЛЭЌЕФЗНЗЈзїRtЁїABCЃЌЪЙЦфаББпAB=cЃЌвЛЬѕжБНЧБпBC=aЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉ
ЁОД№АИЁПЃЈ1ЃЉШчЭМЫљЪОМћНтЮіЃЛЃЈ2ЃЉШчЭМЫљЪОМћНтЮіЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉСЌНсAFЁЂBEЃЌзїЙ§AFгыBEЕФНЛЕуКЭдВаФOЕФжБЯпМДПЩЕУГіСгЛЁ![]() ЕФжаЕуPЃЌИУжБЯпгыдВOдкжБЯпABЯТЗННЛгквЛЕуЃЌзїЙ§ИУЕуКЭHЕуЕФжБЯпгыжБЯпABНЛгквЛЕуЃЌМДЮЊЫљЧѓЕФGЕуЃЛ
ЕФжаЕуPЃЌИУжБЯпгыдВOдкжБЯпABЯТЗННЛгквЛЕуЃЌзїЙ§ИУЕуКЭHЕуЕФжБЯпгыжБЯпABНЛгквЛЕуЃЌМДЮЊЫљЧѓЕФGЕуЃЛ
ЃЈ2ЃЉЗНЗЈвЛИљОнжБОЖЫљЖдЕФдВжмНЧЮЊжБНЧЃЌЯШвдABЮЊжБОЖзїдВЃЌдйвдBЮЊдВаФЃЌaЮЊАыОЖзїдВПЩШЗЖЈCЕуЃЌМДПЩЕУRtЁїABCЃЛЗНЗЈЖўРћгУзїДЙЯпЕФЗНЗЈвдCЕуЮЊДЙзузїжБЯп![]() ЃЌдйвдBЮЊдВаФЃЌcЮЊАыОЖзїдВПЩШЗЖЈAЕуЃЌМДПЩЕУRtЁїABCЃЎ
ЃЌдйвдBЮЊдВаФЃЌcЮЊАыОЖзїдВПЩШЗЖЈAЕуЃЌМДПЩЕУRtЁїABCЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЫљЪОЃЌЕуPЁЂЕуGМДЮЊЫљЧѓЃЛ
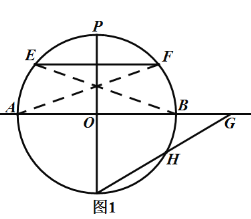
ЃЈ2ЃЉЗНЗЈвЛЃК ШчЭМ2ЫљЪОЃЌRtЁїABCМДЮЊЫљЧѓЃЛ
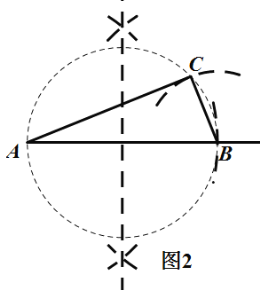
ЗНЗЈЖўЃКШчЭМ3ЫљЪОЃЌRtЁїABCМДЮЊЫљЧѓЃЎ


 гІгУЬтзївЕБОЯЕСаД№АИ
гІгУЬтзївЕБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНax2+bx+3ЃЈaЁй0ЃЉгыxжсЗжБ№НЛгкAЃЈЉ3ЃЌ0ЃЉЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпЕФЖЅЕуEЃЈЉ1ЃЌ4ЃЉЃЌЖдГЦжсНЛxжсгкЕуFЃЎ
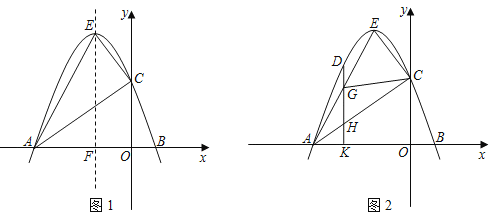
ЃЈ1ЃЉЧыжБНгаДГіетЬѕХзЮяЯпКЭжБЯпAEЁЂжБЯпACЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгACЁЂAEЁЂCEЃЌХаЖЯЁїACEЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕуDЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЫќЕФКсзјБъЮЊmЃЌЧвЉ3ЃМmЃМЉ1ЃЌЙ§ЕуDзїDKЁЭxжсгкЕуKЃЌDKЗжБ№НЛЯпЖЮAEЁЂACгкЕуGЁЂHЃЎдкЕуDЕФдЫЖЏЙ§ГЬжаЃЌ
ЂйDGЁЂGHЁЂHKетШ§ЬѕЯпЖЮФмЗёЯрЕШЃПШєЯрЕШЃЌЧыЧѓГіЕуDЕФзјБъЃЛШєВЛЯрЕШЃЌЧыЫЕУїРэгЩЃЛ
ЂкдкЂйЕФЬѕМўЯТЃЌХаЖЯCGгыAEЕФЪ§СПЙиЯЕЃЌВЂжБНгаДГіНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЦфжа
ЃЌЦфжа![]() гы
гы![]() ГЩЗДБШР§
ГЩЗДБШР§![]() гы
гы![]() ГЩе§БШР§ЃЌКЏЪ§ЕФздБфСП
ГЩе§БШР§ЃЌКЏЪ§ЕФздБфСП![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃЌЧвЕБ
ЃЌЧвЕБ![]() Лђ
Лђ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕОљЮЊ
ЕФжЕОљЮЊ![]() ЁЃ
ЁЃ
ЧыЖдИУКЏЪ§МАЦфЭМЯѓНјааШчЯТЬНОПЃК
ЃЈ1ЃЉНтЮіЪНЬНОПЃКИљОнИјЖЈЕФЬѕМўЃЌПЩвдШЗЖЈГіИУКЏЪ§ЕФНтЮіЪНЮЊЃК ЃЎ
ЃЈ2ЃЉКЏЪ§ЭМЯѓЬНхГЃКЂйИљОнНтЮіЪНЃЌбЁШЁЪЪЕБЕФздБфСП![]() ЃЌВЂЭъГЩЯТБэЃК
ЃЌВЂЭъГЩЯТБэЃК
|
| ЃЎЃЎЃЎ | ||||||||
| ЃЎЃЎЃЎ |
ЂкИљОнБэжаЪ§ОнЃЌдкШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕжаУшЕуЃЌВЂЛГіКЏЪ§ЭМЯѓЃЎ
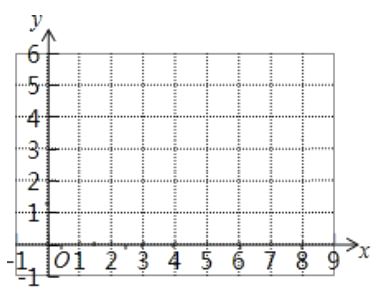
ЃЈ3ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃК
ЂйЕБ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪБЃЌКЏЪ§жЕЗжБ№ЮЊ
ЪБЃЌКЏЪ§жЕЗжБ№ЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЕФДѓаЁЙиЯЕЮЊЃК ЃЈгУЁА
ЕФДѓаЁЙиЯЕЮЊЃК ЃЈгУЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁББэЪОЃЉ
ЁББэЪОЃЉ
ЂкШєжБЯп![]() гыИУКЏЪ§ЭМЯѓгаСНИіНЛЕуЃЌдђ
гыИУКЏЪ§ЭМЯѓгаСНИіНЛЕуЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧ ЃЌДЫЪБЃЌ
ЕФШЁжЕЗЖЮЇЪЧ ЃЌДЫЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЪЧ ЃЎ
ЕФШЁжЕЗЖЮЇЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃПЊеЙЁАЮвзюЯВАЎЕФвЛЯюЬхг§ЛюЖЏЁБЕїВщЃЌвЊЧѓУПУћбЇЩњБибЁЧвжЛФмбЁвЛЯюЃЌЯжЫцЛњГщВщСЫmУћбЇЩњЃЌВЂНЋЦфНсЙћЛцжЦГЩВЛЭъећЕФЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЎ
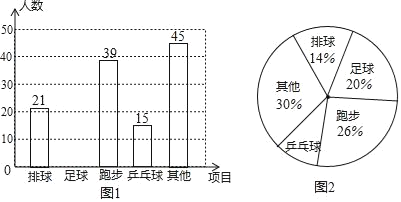
НсКЯвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉmЃНЁЁ ЁЁЃЎ
ЃЈ2ЃЉЧыВЙШЋЩЯУцЕФЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉдкЭМ2жаЃЌЦЙХвЧђЫљЖдгІЩШаЮЕФдВаФНЧЃНЁЁ ЁЁЃЛ
ЃЈ4ЃЉвбжЊИУаЃЙВга2100УћбЇЩњЃЌЧыФуЙРМЦИУаЃдМгаЖрЩйУћбЇЩњзюЯВАЎзуЧђЛюЖЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁбOЕФАыОЖЪЧ2ЃЌЕуAЃЌBдкЁбOЩЯЃЌЧвЁЯAOBЃН90ЁуЃЌЖЏЕуCдкЁбOЩЯдЫЖЏЃЈВЛгыAЃЌBжиКЯЃЉЃЌЕуDЮЊЯпЖЮBCЕФжаЕуЃЌСЌНгADЃЌдђЯпЖЮADЕФГЄЖШзюДѓжЕЪЧ_______ЃЎ
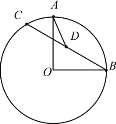
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
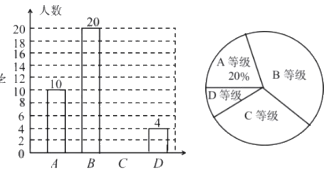
ЁОЬтФПЁПЙўЪаФГжабЇЮЊСЫНтОХФъМЖбЇЩњЬхФмзДПіЃЌДгОХФъМЖбЇЩњжаЫцЛњГщШЁВПЗжбЇЩњНјааЬхФмВтЪдЃЌВтЪдНсЙћЭтЮЊAЁЂBЁЂCЁЂDЫФИіЕШМЖЃЌЧыИљОнСНЗљЭГМЦЭМжаЕФаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮГщбљЕїВщЙВГщШЁСЫЖрЩйУћбЇЩњЃП
ЃЈ2ЃЉЭЈЙ§МЦЫуВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєОХФъМЖЙВга600УћбЇЩњЃЌЧыФуЙРМЦОХФъМЖбЇЩњжаЬхФмВтЪдНсЙћЮЊDЕШМЖЕФбЇЩњгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЖўДЮКЏЪ§yЃНax2+bx+cЕФЭМЯѓЕФвЛВПЗжЃЌЖдГЦжсЪЧжБЯпxЃН1ЃЎ
Ђйb2ЃО4acЃЛ Ђк4a+2b+cЃМ0ЃЛЂлВЛЕШЪНax2+bx+cЃО0ЕФНтМЏЪЧxЁн3.5ЃЛЂмШєЃЈЉ2ЃЌy1ЃЉЃЌЃЈ5ЃЌy2ЃЉЪЧХзЮяЯпЩЯЕФСНЕуЃЌдђy1ЃМy2ЃЎЩЯЪі4ИіХаЖЯжаЃЌе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
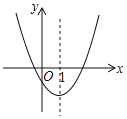
A.ЂйЂкB.ЂйЂкЂмC.ЂйЂлЂмD.ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯAOBЃН60ЁуЃЌАыОЖЮЊ2![]() ЕФЁбMгыБпOAЁЂOBЯрЧаЃЌШєНЋЁбMЫЎЦНЯђзѓЦНвЦЃЌЕБЁбMгыБпOAЯрНЛЪБЃЌЩшНЛЕуЮЊEКЭFЃЌЧвEFЃН6ЃЌдђЦНвЦЕФОрРыЮЊ____ЃЎ
ЕФЁбMгыБпOAЁЂOBЯрЧаЃЌШєНЋЁбMЫЎЦНЯђзѓЦНвЦЃЌЕБЁбMгыБпOAЯрНЛЪБЃЌЩшНЛЕуЮЊEКЭFЃЌЧвEFЃН6ЃЌдђЦНвЦЕФОрРыЮЊ____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
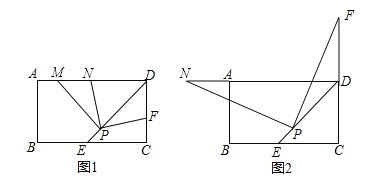
ЁОЬтФПЁПОиаЮABCDжаЃЌDEЦНЗжЁЯADCНЛBCБпгкЕуEЃЌPЮЊDEЩЯЕФвЛЕуЃЈPEЃМPDЃЉЃЌPMЁЭPDЃЌPMНЛADБпгкЕуMЃЎ
ЃЈ1ЃЉШєЕуFЪЧБпCDЩЯвЛЕуЃЌТњзуPFЁЭPNЃЌЧвЕуNЮЛгкADБпЩЯЃЌШчЭМ1ЫљЪОЃЎ
ЧѓжЄЃКЂйPN=PFЃЛЂкDF+DN=![]() DPЃЛ
DPЃЛ
ЃЈ2ЃЉШчЭМ2ЫљЪОЃЌЕБЕуFдкCDБпЕФбгГЄЯпЩЯЪБЃЌШдШЛТњзуPFЁЭPNЃЌДЫЪБЕуNЮЛгкDAБпЕФбгГЄЯпЩЯЃЌШчЭМ2ЫљЪОЃЛЪдЮЪDFЃЌDNЃЌDPгадѕбљЕФЪ§СПЙиЯЕЃЌВЂМгвджЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com