
【题目】已知函数![]() ,其中
,其中![]() 与
与![]() 成反比例
成反比例![]() 与
与![]() 成正比例,函数的自变量
成正比例,函数的自变量![]() 的取值范围是
的取值范围是![]() ,且当
,且当![]() 或
或![]() 时,
时,![]() 的值均为
的值均为![]() 。
。
请对该函数及其图象进行如下探究:
(1)解析式探究:根据给定的条件,可以确定出该函数的解析式为: .
(2)函数图象探宄:①根据解析式,选取适当的自变量![]() ,并完成下表:
,并完成下表:
|
| ... | ||||||||
| ... |
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出函数图象.
(3)结合画出的函数图象,解决问题:
①当![]() ,
,![]() ,
,![]() 时,函数值分别为
时,函数值分别为![]() ,则
,则![]() 的大小关系为: (用“
的大小关系为: (用“![]() ”或“
”或“![]() ”表示)
”表示)
②若直线![]() 与该函数图象有两个交点,则
与该函数图象有两个交点,则![]() 的取值范围是 ,此时,
的取值范围是 ,此时,![]() 的取值范围是 .
的取值范围是 .
【答案】(1)![]() ;(2)见解析;(3)①
;(2)见解析;(3)①![]() ②
②![]() ,
,![]() 且
且![]()
【解析】
(1)由题意用待定系数法设设![]() ,则有
,则有![]() ,将已知条件代入得关于k1、k2方程组,即可求得该函数解析式;
,将已知条件代入得关于k1、k2方程组,即可求得该函数解析式;
(2)①根据题意选取适当数值填表即可;
②在平面直角坐标系中描点,用平滑曲线从左到右顺次连接各点,画出图象;
(3)①由题意结合画出的函数图象运用增减性进行分析即可;
②根据题意观察图象得:x≥![]() ,图象最低点为(2,1),依次进行分析即可.
,图象最低点为(2,1),依次进行分析即可.
解:(1)设![]() ,则有
,则有![]() ,
,
由题意得: ,解得:
,解得: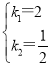 ,
,
∴该函数解析式为:![]() .
.
(2)①根据解析式,补全下表:

②根据上表在平面直角坐标系中描点,画出图象:
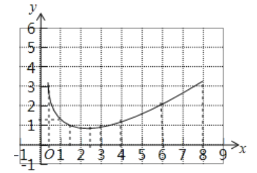
(3)①由(2)中图象可得:(2,1)是图象上最低点,在该点左侧,y随x增大而减小;在该点右侧y随x增大而增大,
∴![]() ,
,
故答案为:![]() ,
,
②观察图象得:x≥![]() ,图象最低点为(2,1),
,图象最低点为(2,1),
∴当直线y=k与该图象有两个交点时,1<k≤![]() ,
,
此时x的范围是:![]() 且
且![]() .
.
故答案为:1<k≤![]() ,
,![]() 且
且![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,4),双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE.
的图像经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式.
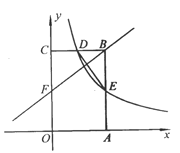
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数![]() 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )

A.3 B.4 C.6 D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为![]() 的
的![]() 中,点
中,点![]() 是劣弧
是劣弧![]() 的中点,点
的中点,点![]() 是优弧
是优弧![]() 上一点,
上一点,![]() ,下列四个结论:①
,下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是菱形.其中正确结论的序号是( )
是菱形.其中正确结论的序号是( )
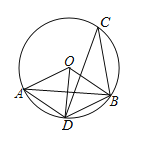
A.①③B.②④C.②③④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() 三个点.
三个点.
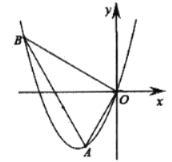
(1)求抛物线解析式;
(2)若点![]() ,
,![]() 为该抛物线上的两点,且
为该抛物线上的两点,且![]() .求
.求![]() 的取值范围;
的取值范围;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() (不与点
(不与点![]() ,点
,点![]() 重合),使点
重合),使点![]() ,点
,点![]() 到直线
到直线![]() 的距离之和最大?若存在,求
的距离之和最大?若存在,求![]() 的度数,并直接写出点
的度数,并直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,AB=AC=3![]() ,在△ABC内作第1个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第2个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第3个内接正方形…,依次进行下去,则第2019个内接正方形的边长为_____.
,在△ABC内作第1个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第2个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第3个内接正方形…,依次进行下去,则第2019个内接正方形的边长为_____.
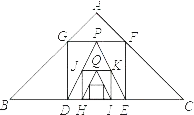
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=50°,连接BD,CE交于点F.填空:
①的值为 ;②∠BFC的度数为 .
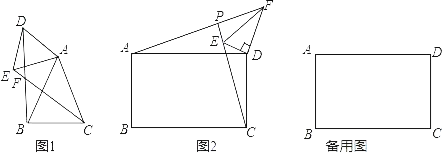
(2)类比探究
如图2,在矩形ABCD和△DEF中,AD=![]() AB,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点P.求
AB,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点P.求![]() 的值及∠APC的度数,并说明理由;
的值及∠APC的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△DEF绕点D在平面内旋装,AF,CE所在直线交于点P,若DF=![]() ,AB=
,AB=![]() ,求出当点P与点E重合时AF的长.
,求出当点P与点E重合时AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在⊙O中,AB是直径,弦EF∥AB,在直径AB下方的半圆上有一个定点H(点H不与点A,B重合),请仅用无刻度的直尺画出劣弧![]() 的中点P,并在直线AB上画出点G,使直线AB平分∠HGP.(保留作图痕迹,不写作法)
的中点P,并在直线AB上画出点G,使直线AB平分∠HGP.(保留作图痕迹,不写作法)


(2)尺规作图:如图2,已知线段a、c,请你用两种不同的方法作Rt△ABC,使其斜边AB=c,一条直角边BC=a.(保留作图痕迹,不写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B,DE交AC于点E.
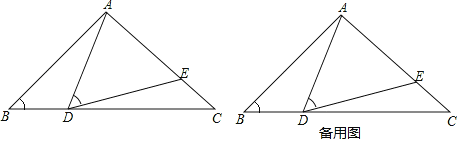
(1)求证:△ABD∽△DCE;
(2)若△DCE为直角三角形,求BD.
(3)若以AE为直径的圆与边BC相切,求AD;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com