
����Ŀ����1�����ⷢ��
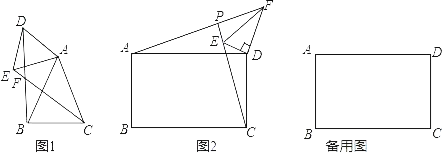
��ͼ1������ABC����ADE�У�AB��AC��AD��AE����BAC����DAE��50��������BD��CE���ڵ�F����գ�
�ٵ�ֵΪ�� �����ڡ�BFC�Ķ���Ϊ�� ����
��2�����̽��
��ͼ2���ھ���ABCD����DEF�У�AD��![]() AB����EDF��90������DEF��60��������AF��CE���ӳ����ڵ�P����
AB����EDF��90������DEF��60��������AF��CE���ӳ����ڵ�P����![]() ��ֵ����APC�Ķ�������˵�����ɣ�
��ֵ����APC�Ķ�������˵�����ɣ�
��3����չ����
�ڣ�2���������£�����DEF�Ƶ�D��ƽ������װ��AF��CE����ֱ�߽��ڵ�P����DF��![]() ��AB��
��AB��![]() ���������P���E�غ�ʱAF�ij���
���������P���E�غ�ʱAF�ij���
���𰸡���1��1��50������2��![]() �����ɼ���������3������P���E�غ�ʱ��AF�ij�Ϊ3��6�����ɼ�����
�����ɼ���������3������P���E�غ�ʱ��AF�ij�Ϊ3��6�����ɼ�����
��������
��1�����ⷢ�֣��ɡ�SAS����֤��DAB�ա�EAC���ɵ�BD��CE����ACE����ABD��������⣻
��2�����̽����ͨ��֤����ADF�ס�CDE���ɵ�![]() ����FAD��DCE��������⣻
����FAD��DCE��������⣻
��3����չ���죺����C��CM��DE���ɹ��ɶ�������CE�ij���������AF�ij���
��1�����ⷢ�֣�
�ߡ�BAC����DAE��50����
���DAB����EAC����AB��AC��AD��AE
���DAB�ա�EAC��SAS��
��BD��CE����ACE����ABD
��![]()
�ߡ�BAC+��ABC+��ACB��180�����ҡ�BFC+��FBC+��FCB����BFC+��ABC+��ABF+��FCB����BFC+��ABC+��ACB��180��
���BFC����BAC��50��
�ʴ�Ϊ1��50��
��2�����̽����
![]() ����APC��90��
����APC��90��
�������£��ߡ�DEF��60������FDE��90��
��DF��![]() DE��
DE��
���ı���ABCD�Ǿ���
��CD��AB����ADC��90��
��AD��![]() DC����ADC����EDF��90��
DC����ADC����EDF��90��
���EDC����ADF����![]()
���ADF�ס�CDE
��![]() ����FAD��DCE
����FAD��DCE
���A����P����D����C�ĵ㹲Բ
���APC����ADC��90��
��3����չ���죺
��ͼ������C��CM��DE����ED�ӳ����ڵ�M��
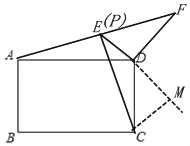
��DF��![]() ����DEF��60������AEC��90��
����DEF��60������AEC��90��
��DE��1����CEM��30��
�ߡ�CEM��30����CM��ED
��![]()
��CD2��CM2+DM2��
��7��![]() +��EM��1��2��
+��EM��1��2��
��CE��2![]()
��![]() ��
��
��AF��6
��ͼ������C��CM��DE����DE�ӳ����ڵ�M��
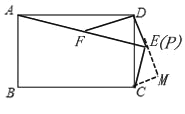
��DF��![]() ����DEF��60������AEC��90��
����DEF��60������AEC��90��
��DE��1����CEM��30��
�ߡ�CEM��30����CM��ED
��![]()
��CD2��CM2+DM2��
��7��![]() +��EM+1��2��
+��EM+1��2��
��CE��![]()
��![]() ��
��
��AF��3
��������������P���E�غ�ʱ��AF�ij�Ϊ3��6��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
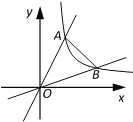
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����������![]() ������������
������������![]() ��ͼ��ֱ��ڵ�A��B������AOB��45�������AOB�������________��
��ͼ��ֱ��ڵ�A��B������AOB��45�������AOB�������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
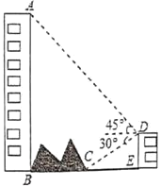
����Ŀ����ͼ����¥���Ҳ���һ�ϰ�����ϰ�����Ա���һ��С¥DE����С¥�Ķ���D������ϰ����Ե��C�ĸ���Ϊ30������ô�¥����A������Ϊ45������B��C��E��ͬһˮƽֱ���ϣ�.��֪AB=80m��DE=20m�����ϰ���B��C�����ľ���.������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ��
��![]() �ɷ�����
�ɷ�����![]() ��
��![]() �����������������Ա���
�����������������Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ���ҵ�
���ҵ�![]() ��
��![]() ʱ��
ʱ��![]() ��ֵ��Ϊ
��ֵ��Ϊ![]() ��
��
��Ըú�������ͼ���������̽����
��1������ʽ̽�������ݸ���������������ȷ�����ú����Ľ���ʽΪ�� ��
��2������ͼ��̽峣��ٸ��ݽ���ʽ��ѡȡ�ʵ����Ա���![]() ��������±���
��������±���
|
| ������ | ||||||||
| ������ |
�ڸ��ݱ������ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬����������ͼ��
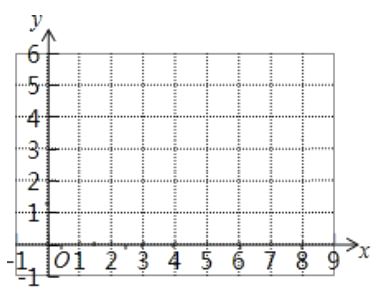
��3����ϻ����ĺ���ͼ������⣺
�ٵ�![]() ��
��![]() ��
��![]() ʱ������ֵ�ֱ�Ϊ
ʱ������ֵ�ֱ�Ϊ![]() ����
����![]() �Ĵ�С��ϵΪ�� ������
�Ĵ�С��ϵΪ�� ������![]() ������
������![]() ����ʾ��
����ʾ��
����ֱ��![]() ��ú���ͼ�����������㣬��
��ú���ͼ�����������㣬��![]() ��ȡֵ��Χ�� ����ʱ��
��ȡֵ��Χ�� ����ʱ��![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
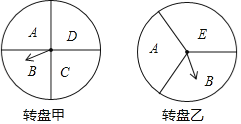
����Ŀ��ij�����ڶ�����ڼ俪չ�Żݻ���������߿���ͨ��ת��ת�̵ķ�ʽ�����ۿ��Żݣ����λ�������ַ�ʽ����ʽһ��ת��ת�̼ף�ָ��ָ��A����ʱ����������Ʒ����9���Żݡ�ָ��ָ�������������Żݣ���ʽ����ͬʱת��ת�̼�ת���ң�������ת�̵�ָ��ָ��ÿ���������ĸ��ͬ����������Ʒ����8���Żݣ�����������Żݣ���ÿ��ת���У�ָ��ָ��ÿ�����ǵĿ�������ͬ����ָ��ָ��ֽ��ߣ�������ת��ת�̣�
��1�����˿�ѡ��ʽһ��������9���Żݵĸ���Ϊ������
��2�����˿�ѡ��ʽ����������״ͼ���б����г����п��ܣ�����˿�����8���Żݵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չ������ϲ����һ������������飬Ҫ��ÿ��ѧ����ѡ��ֻ��ѡһ�����������m��ѧ���������������Ƴɲ�����������ͳ��ͼ������ͳ��ͼ��
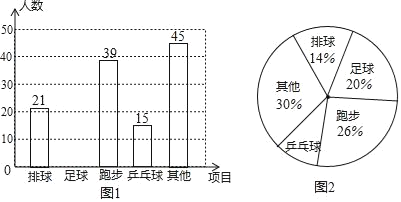
���������Ϣ����������⣺
��1��m���� ����
��2���벹ȫ���������ͳ��ͼ��
��3����ͼ2�У�ƹ��������Ӧ���ε�Բ�Ľǣ��� ����
��4����֪��У����2100��ѧ����������Ƹ�УԼ�ж�����ѧ����ϲ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
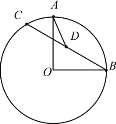
����Ŀ����ͼ����֪��O�İ뾶��2����A��B�ڡ�O�ϣ��ҡ�AOB��90��������C�ڡ�O���˶�������A��B�غϣ�����DΪ�߶�BC���е㣬����AD�����߶�AD�ij������ֵ��_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
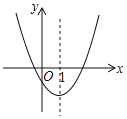
����Ŀ����ͼ�Ƕ��κ���y��ax2+bx+c��ͼ���һ���֣��Գ�����ֱ��x��1��
��b2��4ac�� ��4a+2b+c��0��������ʽax2+bx+c��0�Ľ⼯��x��3.5����������2��y1������5��y2�����������ϵ����㣬��y1��y2������4���ж��У���ȷ���ǣ�������
A.�٢�B.�٢ڢ�C.�٢ۢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ÿ��С�����α߳�Ϊ1�������У���A��B��C���ڸ���ϣ�
����AC�ij��ȵ���_____��
��������ͼ����һ��P��������AP��PB��PC������APƽ�֡�A����PC=PB��������ͼ��ʾ�������У����̶ȵ�ֱ�ߣ�������P������Ҫ˵����P��λ��������ҵ��ģ���Ҫ��֤����_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com