
【题目】请仅用无刻度直尺完成下列画图,不写画法,保留画图痕迹.
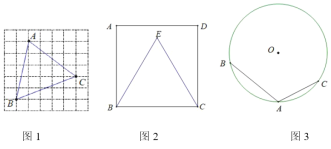
(1)如图1,在![]() 的正方形网格中,每个小正方形的边长为1,小正方形的顶点叫做格点.
的正方形网格中,每个小正方形的边长为1,小正方形的顶点叫做格点.![]() 的顶点在格点上,过点
的顶点在格点上,过点![]() 画一条直线平分
画一条直线平分![]() 的面积;
的面积;
(2)如图2,点![]() 在正方形
在正方形![]() 的内部,且
的内部,且![]() ,过点
,过点![]() 画一条射线平分
画一条射线平分![]() ;
;
(3)如图3,点![]() 、
、![]() 、
、![]() 均在
均在![]() 上,且
上,且![]() ,在优弧
,在优弧![]() 上画
上画![]() 、
、![]() 两点,使
两点,使![]() .
.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)找出以BC为对角线的矩形BECD,连接DE,交BC于点O,作直线AO即可;
(2)连接AC、BD交于点O,作射线EO即可;
(3)连接BO并延长交![]() 于点N,连接AN,连接CO并延长交
于点N,连接AN,连接CO并延长交![]() 于点M,连接AM,根据直径所对的圆周角是直角即可得出结论.
于点M,连接AM,根据直径所对的圆周角是直角即可得出结论.
解:(1)如图所示,找出以BC为对角线的矩形BECD,连接DE,交BC于点O,作直线AO,根据矩形的性质可得O为BC的中点,根据中线的性质可得直线AO平分![]() 的面积,故AO即为所求;
的面积,故AO即为所求;

(2)连接AC、BD交于点O,作射线EO,根据正方形的性质可得OB=OC

∵四边形ABCD为正方形
∴OB=OC
∴点O在BC的中垂线上,
∵EB=EC
∴点E在BC的中垂线上
∴EO垂直平分BC
∴射线EO平分![]() ,射线EO即为所求;
,射线EO即为所求;
(3)连接BO并延长交![]() 于点N,连接AN,连接CO并延长交
于点N,连接AN,连接CO并延长交![]() 于点M,连接AM
于点M,连接AM
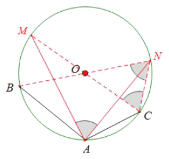
∵BN和CM都为![]() 的直径,
的直径,
∴∠BAN=∠CAM=90°
∵![]()
∴∠BAM=∠BAC-∠CAM=30°,
∴∠MAN=∠BAN-∠BAM=60°
∴点M、N即为所求.


科目:初中数学 来源: 题型:
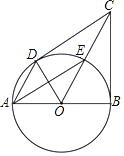
【题目】如图,已知D是⊙O上一点,AB是直径,∠BAD的平分线交⊙O于点E,⊙O的切线BC交OE的延长线于点C,连接OD,CD.
(1)求证:CD⊥OD.
(2)若AB=2,填空:
①当CE= 时,四边形BCDO是正方形.
②作△AEO关于直线OE对称的△FEO,连接BF,BE,当四边形BEOF是菱形时,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】龙虾狂欢季再度开启,第![]() 届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为
届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为![]() 元,在整个销售旺季的
元,在整个销售旺季的![]() 天里,销售单价
天里,销售单价![]() 元/千克,与时间
元/千克,与时间![]() (天)之间的函数关系式为:
(天)之间的函数关系式为: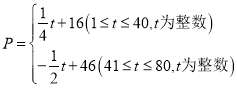 ,日销售量
,日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
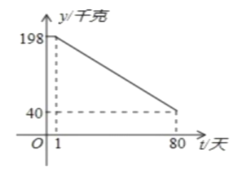
(1)求日销售量![]() 与时间
与时间![]() 的函数关系式?
的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前![]() 天中,该养殖户决定销售
天中,该养殖户决定销售![]() 千克小龙虾,就捐赠
千克小龙虾,就捐赠![]() 元给村里的特困户,在这前
元给村里的特困户,在这前![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=a(x+2)2﹣3与y2=![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=![]() ;③当x=0时,y2﹣y1=6;④AB+AC=10;其中正确结论的个数是( )
;③当x=0时,y2﹣y1=6;④AB+AC=10;其中正确结论的个数是( )
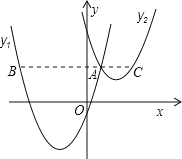
A.①②④B.①③④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 两点在反比例函数
两点在反比例函数![]() 的图象上,下列三个命题:①若
的图象上,下列三个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,
,![]() ,则
,则![]() ;③过
;③过![]() 、
、![]() 两点的直线与
两点的直线与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() ,则
,则![]() .其中真命题个数是( )
.其中真命题个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投掷一次骰子,向上一面的点数记为![]() ,再投掷一次骰子,向上一面的点数记为
,再投掷一次骰子,向上一面的点数记为![]() ,这样就确定点
,这样就确定点![]() 的一个坐标
的一个坐标![]() ,那么点
,那么点![]() 落在双曲线
落在双曲线![]() 上的概率为( )
上的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图:
等级 | 视力(x) | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合计 | 40 | 1 | |
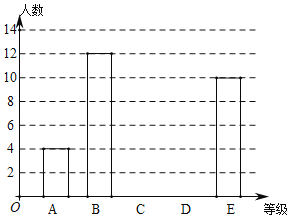
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“![]() 级”的有多少人?
级”的有多少人?
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com