
【题目】如图,在平面直角坐标系中,点![]() 是坐标原点,四边形
是坐标原点,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
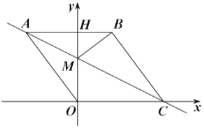
(Ⅰ)求直线![]() 的解析式;
的解析式;
(Ⅱ)动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以2个单位/秒的速度向终点
方向以2个单位/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]()
![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
①当![]() 时,求
时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
②在点![]() 运动过程中,当
运动过程中,当![]() 时,求
时,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成不完整的条形统计图和扇形统计图.
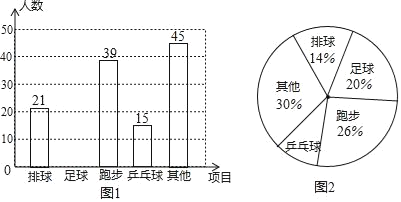
结合以上信息解答下列问题:
(1)m= .
(2)请补全上面的条形统计图;
(3)在图2中,乒乓球所对应扇形的圆心角= ;
(4)已知该校共有2100名学生,请你估计该校约有多少名学生最喜爱足球活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=60°,半径为2![]() 的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为____.
的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
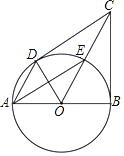
【题目】如图,已知D是⊙O上一点,AB是直径,∠BAD的平分线交⊙O于点E,⊙O的切线BC交OE的延长线于点C,连接OD,CD.
(1)求证:CD⊥OD.
(2)若AB=2,填空:
①当CE= 时,四边形BCDO是正方形.
②作△AEO关于直线OE对称的△FEO,连接BF,BE,当四边形BEOF是菱形时,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长度等于_____;
(Ⅱ)在图中有一点P,若连接AP,PB,PC,满足AP平分∠A,且PC=PB,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
类比定义:我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则等等.小学里,把分子比分母小的分数叫做真分数,类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.
拓展定义:
对于任何一个分式都可以化成整式与真分式的和的形式,
如:![]() ;
;
![]() .
.
理解定义:
(1)下列分式中,属于真分式的是:____属于假分式的是:_____(填序号)
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
拓展应用:
(2)将分式![]() 化成整式与真分式的和的形式;
化成整式与真分式的和的形式;
(3)将假分式![]() 化成整式与真分式的和的形式。
化成整式与真分式的和的形式。
查看答案和解析>>
科目:初中数学 来源: 题型:
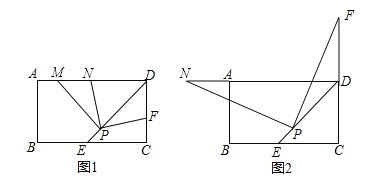
【题目】矩形ABCD中,DE平分∠ADC交BC边于点E,P为DE上的一点(PE<PD),PM⊥PD,PM交AD边于点M.
(1)若点F是边CD上一点,满足PF⊥PN,且点N位于AD边上,如图1所示.
求证:①PN=PF;②DF+DN=![]() DP;
DP;
(2)如图2所示,当点F在CD边的延长线上时,仍然满足PF⊥PN,此时点N位于DA边的延长线上,如图2所示;试问DF,DN,DP有怎样的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】龙虾狂欢季再度开启,第![]() 届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为
届中国合肥龙虾节的主题是“让你知虾,也知稻”,稻田小龙虾养殖技术在合肥周边的乡镇大力推广,已知每千克小龙虾养殖成本为![]() 元,在整个销售旺季的
元,在整个销售旺季的![]() 天里,销售单价
天里,销售单价![]() 元/千克,与时间
元/千克,与时间![]() (天)之间的函数关系式为:
(天)之间的函数关系式为: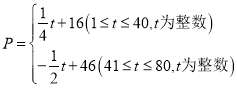 ,日销售量
,日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
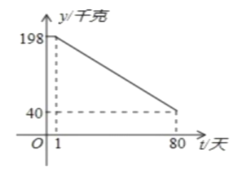
(1)求日销售量![]() 与时间
与时间![]() 的函数关系式?
的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前![]() 天中,该养殖户决定销售
天中,该养殖户决定销售![]() 千克小龙虾,就捐赠
千克小龙虾,就捐赠![]() 元给村里的特困户,在这前
元给村里的特困户,在这前![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com